Работа с формулами: Функции Excel (по категориям) — Служба поддержки Майкрософт

Содержание

Microsoft Word — работа с формулами в ворде

Работа с формулами в Microsoft Word

Многие из Вас просили написать урок о работе с формулами в Word. Откровенно говоря, у меня последний месяц был напряженный в плане работы, но вот я нашел свободный вечерок и решил написать статью. Сегодня мы рассмотрим добавление, работу с формулами, дополнительные редакторы.

Добавление формул

Для добавления новой формулы в Word 2007 необходимо в верхней части сайта перейти в раздел “Вставка” и в самой правой части экрана выбрать пункт “Формула”. Курсор Ваш должен быть установлен на том месте, где сейчас будет вставлена формула.

Вставка новой формулы

Так же есть способ еще быстрее – это, конечно же, горячие клавиши. Добавить область для редактирования формулы можно при помощи сочетания клавиш “ALT + =”. После нажатий форма для редактирования формулы появится на месте Вашего курсора.

Редактирование формул

Для Вашего удобства в Word есть заранее заданные формулы, которые постоянно используются многими людьми. Среди таких формул Вы можете найти квадратное уравнение, ряд Тейлора, ряд Фурье, теорему Пифагора и множество других.

Панель символов

Но если Вам необходимо ввести свою формулу, у Вас есть все инструменты для этого. Во-первых, это панель символов, расположенная в верхней части программы. Если она у Вас вдруг пропала, Вам нужно просто нажать на голубую область справа на месте для формулы.

Структуры формул Word

Во-вторых, для удобства даны различные структуры математических выражений, которые необходимы для создания формул. Там Вы можете выбрать дробь, индекс, радикал, пределы и логарифмы, функции и вставлять различные виды скобок. Данная панель находится справа от панели с символами.

Формулы можно задавать, как в линейном варианте, так и в профессиональном режиме. В линейном формате, считается более простой вариант редактирования формулы.

Удаление формулы

У многих почему-то не удается удалить только что созданную формулу. Возможно, это случается по причине того, что если попытаться поставить курсор после формулы, он встанет непосредственно в формулу. И по этой причине нет возможности нажать “Backspace” и просто стереть её, будут стираться символы в формуле.

Пример формулы

Для удаления формулы Вам нужно нажать один раз левой кнопкой по голубой правой части формулы, тем самым выделив полностью все формулу. Теперь Вам остается только нажать кнопку “DEL” на клавиатуре и формула пропадет из Вашего документа.

Mathtype для Word 2007

Если у Вас есть потребность в профессиональной работе с формуле, тогда хотелось порекомендовать Вам дополнительную программу под названием Mathtype. Это, пожалуй, самый лучший программный комплекс, созданный исключительно для работы с формулами.

Mathtype

Программа работает более, чем с 350 приложениями, в том числе и с Microsoft Word, Excel, Open Office, Google Docs и другими офисными приложениями. В программе содержится более пятисот математических выражений и символов, которые позволят написать любую, даже самую сложную формулу.

Программа платная, полная версия на начало 2016 года стоит от 97 долларов, для образовательных учреждений – 57 долларов. У программы есть бесплатный период использования 30 дней, в течение которого Вы можете работать с ней абсолютно без ограничений. Если Вам понравился данный продукт, рекомендую его купить.

Программа интегрируется в Ваш Microsoft Word и полностью совместима с ним. Можно работать сразу с двумя программами и это очень удобно. Подходит, начиная от версии 2003, и заканчивая самый последней актуальной версией на данный момент.

Официальный сайт программы Mathtype — www.dessci.com

4.3.3. Работа с формулами, диаграммами, списками

Ввод формул. Возможность работы
с формулами и встроенными функциями
является важнейшей особенностью
электронных таблиц. Логика использования
табличного процессора требует применять
формулы везде, где значения одних ячеек
зависят от значений других, т.к. если
значения ячеек с исходными данными
изменяются, то автоматически изменяются
значения всех зависимых ячеек.

Как известно, ввод формулы начинается
со знака равенства и сопровождается
дублированием набора в строке формул,
завершается нажатием клавиши Enter,
после чего, в ячейке появляется результат
вычисления (при настройках процессора
по умолчанию), а саму же формулу теперь
можно увидеть в строке формул, если
активизировать ячейку.

Формула может содержать числовые
константы, ссылки (адреса ячеек, содержимое
которых участвует в вычислениях),
функции. Указанные элементы между собой
могут соединяться знаками арифметических
операций, скобки могут изменять принятый
в арифметике порядок действий.

Например, пусть в ячейке А1 содержится
число 10, в ячейке В1 число 20, в ячейку С1
введем формулу =А1+В1+2. После завершения
ввода (нажатие Enter) в ячейке
С1 появится результат сложения чисел,
содержащихся в ячейках А1 и В1, увеличенный
на 2, т.е. 32. Если изменить число, хранящееся
в ячейке А1, например заменить на 20, то
наличие формулы в ячейке С1 автоматически
изменит ее значение на 42.

Ссылки А1 и В1 в формуле можно делать,
непосредственно вводя с клавиатуры
текст формулы или после знака равенства
сделать щелчок по ячейке А1 (в формуле
появится ссылка А1), набрать знак + ,
сделать щелчок по В1, снова +, набрать 2
.

Автозаполнение ячеек формулами.
Активизируем ячейку С1 из предыдущего
примера и протянем ее за маркер заполнения
вниз по столбцу. В ячейку С2 автоматически
введется формула =А2+В2+2, в С3 =А3+В3+2 и
т.д. При протягивании по столбцу номер
столбца увеличивается. Вернемся в ячейку
С1 и протянем ее по строке, получим: в
ячейке D1 =B1+C1
, в E1 =C1+D1
и т.д. при протягивании по строке номер
строки увеличивается. Таким образом,
при протягивании формулы ссылки А1 и В1
модифицируются, такие ссылки называются
относительными. Чтобы ссылки не
модифицировались при протягивании по
строке, ее следует записать как C$1,
запретить модификацию по столбцу, можно
применив ссылку $C1. Ссылка
будет неизменна при любом протягивании
в виде $C$1. Такие ссылки
называются абсолютными.

В длинных математических расчетах по
формулам, как правило, исходные данные
содержатся в ячейках, которые в дальнейшем
используются как абсолютные ссылки.
Весьма неудобно было бы постоянно
помнить, в каких ссылках какие параметры
находятся (например, в $C$1
находится параметр b, в
$D$147 – k и
т. п.). Для этого в Excel есть возможность
переименования абсолютных ссылок. Меню
ВСТАВКА►ИМЯ►ПРИСВОИТЬ вызывает
диалоговое окно, в котором можно
абсолютную ссылку переименовать. В том
же меню при необходимости можно удалить
уже существующее имя.

Ссылки на другие листы и книги. Для
обращения к значению ячейки, расположенной
на другом рабочем листе, нужно указать
имя этого листа вместе с адресом
соответствующей ячейки. Например,
находясь на листе 1можно ввести в ячейку
А1 формулу

=ЛИСТ4!B3+1 для обращения к ячейке В3 на
рабочем листе ЛИСТ4. Если в названии
листа есть пробелы, то оно (название)
заключается в кавычки. Связывание двух
ячеек можно упростить, для чего на листе
1 в ячейке А1 набрать знак = , затем через
корешок обратиться к листу 4 и щелкнуть
по ячейке В3.

Копирование ячеек, содержащих
формулы. Техника копирования,
перемещения, удаления ячеек, содержащих
формулы, такая же, как и ячеек, содержащих
данные (см 4. 2.2.) Но, если в формуле
содержатся относительные ссылки, то
при копировании и перемещении они
модифицируются. Рассмотрим на примере.
Пусть в ячейке С3 содержится формула
= А1+$B1+C$1+$D$1.
Перенесем или скопируем ее в ячейку
E6, — т.е. на два столбца
правей и на три строки ниже. Тогда все
относительные адреса формулы в ячейке
Е6 увеличатся на два по столбцу, на три
по строке. В результате в ячейке Е6
получим формулу =C4+$B4+E$1+$D$1.

Работа с функциями. Excel позволяет
использовать в формулах ряд встроенных
математических, логических, статистических
функций. Функции
объединяют несколько
вычислительных операций для решения
определенной задачи, имеют один или
несколько аргументов. В качестве
аргументов функций выступают числовые
значения и/или адреса ячеек.

Вызывается функция как правило
с помощью МАСТЕРА ФУНКЦИЙ меню ВСТАВКА
или кнопки
.
Диалоговое окно «Мастера функций» имеет
два шага. На первом шаге выбрается тип
функции в поле «Категория», затем сама
функция в списке «Функция». Следующий
шаг уточняет аргументы.

Диаграммы.
Диаграмма
– это представление данных таблицы в
графическом виде, которое используется
для анализа и сравнения данных. На
диаграмме числовые данные ячеек
изображаются в виде точек, линий, полос,
столбиков, секторов и в другой форме.
Группы элементов данных, отражающих
содержимое ячеек одной строки или
столбца на рабочем листе, составляют
ряд данных. Строятся диаграммы с помощью
Мастера диаграмм. Вызывается через меню
ВСТАВКА►ДИАГРАММА или нажатием кнопки

на панели инструментов «Стандартная».
Мастер имеет четыре шага, где выясняются
вопросы о виде диаграммы, особенностях
оформления и размещения, затем строится
диаграмма.

Списки.
Списки
позволяют эффективно работать с большими
упорядоченными наборами данных, имеющих
одинаковую структуру. Например, списком
является телефонный справочник, в
котором в большом количестве строк
приведены фамилии абонентов и номера
их телефонов. Каждый элемент списка
занимает одну строку, в которой данные
распределяются по нескольким полям
(столбцам). В табличном процессоре
имеются операции для их обработки
(сортировка, фильтрация).

В первой строке рабочего листа обычно
помещаются названия отдельных полей
списка. Эта строка используется в
качестве строки заголовков списка.
Начиная со следующей строки, вводятся
данные.

Для быстрого заполнения таблицы можно
обратиться к меню ДАННЫЕ►ФОРМА, которое,
откроет диалоговое окно для ввода
данных, в котором каждому полю списка
соответствует поле ввода. Как только
все поля ввода будут заполнены данными,
щелкнем по командной кнопке ДОБАВИТЬ.
Затем можно начать ввод следующего
элемента данных и т.д., пока не будут
введены все элементы списка. В заключение
закроем окно щелчком по командной кнопке
ЗАКРЫТЬ. Каждый новый список следует
создавать на отдельном рабочем листе.

Фильтрация данных. Выделим
заголовки списка. Откроем в меню
ДАННЫЕ►ФИЛЬТР►АВТОФИЛЬТР. В таблице
рядом с названиями полей появятся
маленькие пиктограммы со стрелками
.
Как известно, это раскрывающиеся списки

Рис. 4.11. Раскрывающиеся списки

Щелкнув по одной из этих стрелок, получим
меню с перечнем значений данного поля.

Рис. 4.12. Перечень значений поля.

Щелчком выберем какой-либо пункт из
этого перечня. В списке отобразятся
только те элементы, у которых значение
данного поля совпадает с выбранным
значением, т.е. произойдет фильтрация
данных. При этом пиктограмма со стрелкой
будет изображена другим цветом. Слева
в столбце с номерами строк будут видны
прежние номера элементов, которые они
имели в исходном списке.

Если необходимо вернуться к полному
списку, то нужно выбрать опцию ВСЕ в
перечне значений поля, по которому
выполнялась фильтрация. Здесь же есть
опция УСЛОВИЕ, позволяющая задать
условие фильтрации. Например, выбрать
все записи, значение поля у которых
больше 10 и т. п.

Сортировка данных. Активизируем
первую ячейку в столбце «Фамилия».
Выберем меню ДАННЫЕ►СОРТИРОВКА.
Откроется диалоговое окно этой директивы,
в котором указываются поля сортировки
и рядом с каждым полем расположены две
селекторные кнопки ПО ВОЗРАСТАНИЮ и ПО
УБЫВАНИЮ, указывающие направление
сортировки.

Печать.
Перед распечаткой таблиц необходимо
установить параметры страницы с помощью
команды меню ФАЙЛ►ПАРАМЕТРЫ СТРАНИЦЫ.
Эта процедура во многом сходна с Word.
Отличие в лишь том, что таблица здесь
может быть распечатана в масштабе. Для
этого включим переключатель УСТАНОВИТЬ
и укажем масштаб распечатки. Если
включить переключатель РАЗМЕСТИТЬ НЕ
БОЛЕЕ ЧЕМ НА, то таблица или выделенная
область будет уменьшена настолько,
чтобы разместиться на количестве
страниц, указанном в полях СТР. В ШИРИНУ
и СТР. В ВЫСОТУ.

Для просмотра таблицы перед печатью
используется команда ФАЙЛ ► ПРЕДВАРИТЕЛЬНЫЙ
ПРОСМОТР или кнопка
.
Выйти из режима предварительного
просмотра можно с помощью кнопки ЗАКРЫТЬ
или клавиши Esc. Для распечатки таблицы
необходимо обратиться в меню ФАЙЛ►ПЕЧАТЬ,
которое имеет такие же настройки как
соответствующая опция в Word. Чтобы
напечатать одну копию активных листов
достаточно щелкнуть кнопку
.

2.6 Работа с формулами — Алгебра среднего уровня

Глава 2. Линейные уравнения

В алгебре часто приходится упрощать выражения, чтобы их было легче использовать. Существует три основных формы упрощения, которые будут рассмотрены здесь. Первая форма упрощения выражений используется, когда известно значение каждой переменной в выражении. В этом случае каждую переменную можно заменить эквивалентным числом, а остальную часть выражения можно упростить, используя порядок операций.

Вычислить [латекс]p(q + 6)[/латекс], когда [латекс]р = 3[/латекс] и [латекс]q = 5.[/латекс]

[латекс]\begin{array}{rl } (3)((5)+(6))&\text{Замените }p\text{ на 3 и }q\text{ на 5 и оцените скобки} \\ (3)(11)&\text{Умножить } \\ 33&\text{Решение} \end{массив}[/latex]

Всякий раз, когда переменная чем-то заменяется, новое число записывается внутри скобок.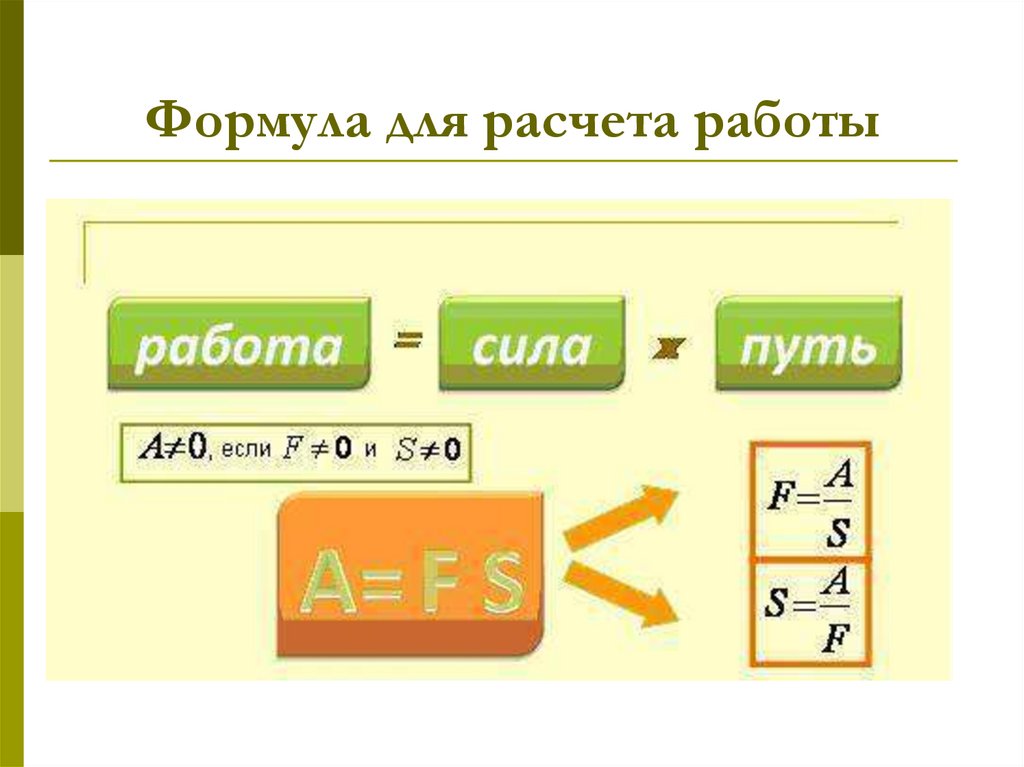 Обратите внимание, что значения 3 и 5 в предыдущем примере заключены в круглые скобки. Это сделано для сохранения операций, которые иногда теряются при простой замене. Иногда круглые скобки не имеют значения, но это хорошая привычка всегда использовать их, чтобы предотвратить проблемы позже.

Вычислить [латекс]x + zx(3 — z)\left(\dfrac{x}{3}\right)[/latex], когда [latex]x = -6[/latex] и [latex]z = — 2.[/latex]

[латекс]\begin{array}{rl} (-6)+(-2)(-6)\left[(3)-(-2)\right]\left(\ dfrac{-6}{3}\right)&\text{Вычислить скобки} \\ \\ -6+(-2)(-6)(5)(-2)&\text{Умножить слева направо} \ \ -6+12(5)(-2)&\text{Умножение слева направо} \\ -6+60(-2) &\text{Умножение} \\ -6-120 & \text{Вычитание} \ \ -126& \text{Решение}\end{массив}[/latex]

Выделение переменных в формулах аналогично решению общих линейных уравнений. Единственная разница в том, что с формулой в задаче будет несколько переменных, и цель состоит в том, чтобы решить для одной конкретной переменной. Например, рассмотрите решение такой формулы, как [латекс]A = \pi r^2+ \pi rs[/латекс] (формула площади поверхности прямого круглого конуса) для переменной [латекс]s. 2}{\pi r}.[/latex] Второе уравнение дает ту же информацию, что и первое; они алгебраически эквивалентны. Однако один решается для площади [латекс]A,[/латекс], а другой — для наклонной высоты конуса [латекс]s.[/латекс]

При решении формулы для переменной сосредоточиться на одной переменной, для которой решается; все остальные обрабатываются так же, как числа. Это показано в следующем примере. Показаны две параллельные задачи: первая представляет собой обычное одношаговое уравнение, а вторая представляет собой формулу, которую вы решаете для [latex]x.[/latex]

Изолируйте переменную [latex]x[/latex] в следующих уравнениях.

[латекс]\begin{array}{ll} \begin{array}{rrl} 3x&=&12 \\ \\ \dfrac{3x}{3}&=&\dfrac{12}{3} \\ \ \ x&=&4 \end{массив} & \hspace{0.5in} \begin{массив}{rrl} wx&=&z \\ \\ \dfrac{wx}{w}&=&\dfrac{z}{w} \\ \\ x&=&\dfrac{z}{w} \end{массив} \end{массив}[/latex]

Для выделения [латекс]x[/латекс] в [латекс]3x = 12[/латекс] используется тот же процесс, что и в [латекс]wx = z. [/латекс]. Поскольку [латекс]х[/латекс] решаем для, относитесь ко всем другим переменным как к числам. Для этих двух уравнений обе части были разделены на 3 и [латекс]w,[/латекс] соответственно. Похожая идея видна в следующем примере.

Изолировать переменную [latex]n[/latex] в уравнении [latex]m+n=p.[/latex]

Чтобы изолировать [latex]n,[/latex] переменную [latex]m[/latex] ] необходимо удалить, что делается путем вычитания [latex]m[/latex] с обеих сторон:

[латекс]\begin{array}{rrrrl} m&+&n&=&p \\ -m&&&&\phantom{p}-m \\ \hline &&n&=&p-m \end{array}[/latex]

Поскольку [латекс]р[/латекс] и [латекс]м[/латекс] не похожи друг на друга, их нельзя комбинировать. По этой причине оставьте выражение как [latex]p — m.[/latex]

.

Изолировать переменную [латекс]а[/латекс] в уравнении [латекс]а(х — у) = b.[/латекс]

Это означает, что [латекс](х-у)[/латекс] должен быть изолирован от переменная [латекс]а.[/латекс]

[латекс]\dfrac{a(xy)}{(xy)}=\dfrac{b}{(xy)}\hspace{0,25 дюйма}\Rightarrow\hspace{0,25 дюйма}a=\dfrac{b} {(х-у)}[/латекс]

Если не решается ни один отдельный термин в круглых скобках, сохраните термины внутри них вместе и разделите на них как единое целое. Однако, если решается отдельный термин внутри круглых скобок, его необходимо распределить. В следующем примере используется та же формула, что и в примере 2.6.5, но на этот раз вычисляется [латекс]x[/латекс].

Изолировать переменную [латекс]х[/латекс] в уравнении [латекс]а(х — у) = b.[/латекс]

Сначала распределите [латекс]а[/латекс] по всему [латексу](x-y)[/латекс]:

[латекс]\begin{array}{rrrrr} a(x&-&y)&=&b \\ ax& -&ay&=&b \end{array}[/latex]

Удалить термин [latex]ay[/latex] с обеих сторон:

[latex]\begin{array}{rrrrl} ax&-&ay&=&b \\ &+&ay&&\phantom{b}+ay \\ \hline &&ax&=&b+ay \end{array}[/latex]

[latex]ax[/latex] затем делится на [latex]a[/latex] :

[латекс]\dfrac{ax}{a}=\dfrac{b+ay}{a}[/latex]

Решение: [latex]x=\dfrac{b+ay}{a},[ /latex], который также может отображаться как [latex]x=\dfrac{b}{a}+y.[/latex]

Будьте очень осторожны при выделении [латекс]x[/латекс] и не пытайтесь отменить [латекс]а[/латекс] в верхней и нижней части дроби.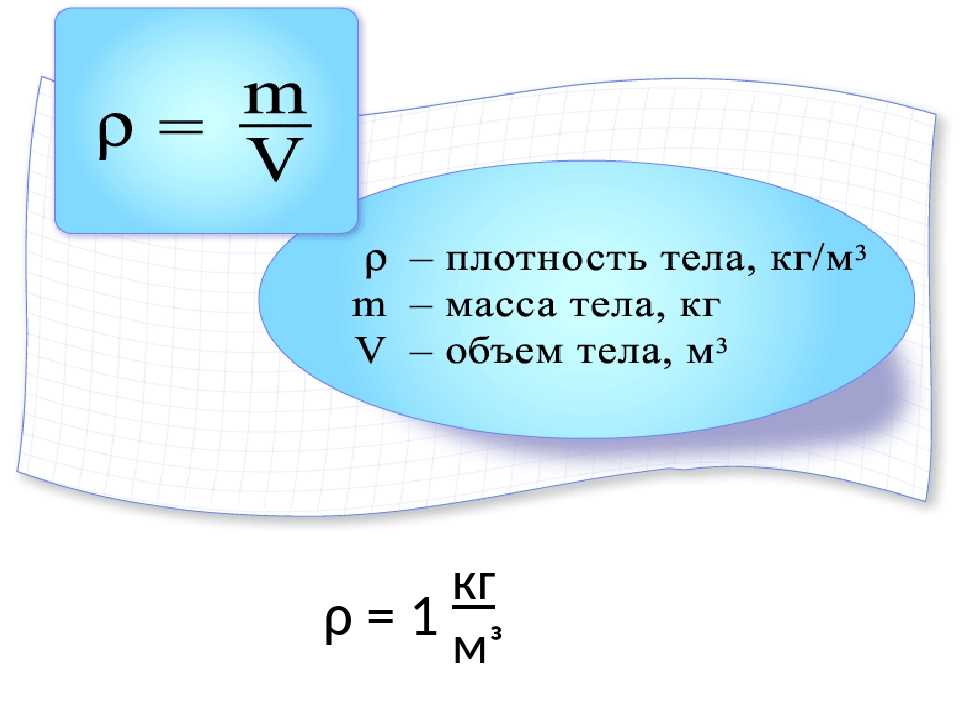 Это не допускается, если в дроби есть какие-либо прибавления или вычитания. В этой задаче невозможна редукция, поэтому окончательный сокращенный ответ остается [latex]x = \dfrac{b + ay}{a}.[/latex] Следующий пример — еще одна двухшаговая задача.

Выделить переменную [латекс]m[/латекс] в уравнении [латекс]у=mx+b.[/латекс]

Сначала вычесть [латекс]b[/латекс] из обеих частей:

[латекс] \begin{array}{lrrrr} y&=&mx&+&b \\ \phantom{y}-b&&&-&b \\ \hline y-b&=&mx&& \end{array}[/latex]

Теперь разделите обе части на [ латекс]x[/латекс]:

[латекс]\dfrac{y-b}{x}=\dfrac{mx}{x}[/latex]

Следовательно, решение [латекс]m=\dfrac{y-b {х}.[/латекс] 92}{\pi г}[/латекс]

Формулы часто содержат дроби и могут быть решены почти так же, как и любая дробь. Сначала определите ЖК, а затем умножьте каждый член на ЖК. После сокращения дробей в задаче больше не будет.

Изолировать переменную [latex]m[/latex] в уравнении [latex]h=\dfrac{2m}{n}.[/latex]

Чтобы очистить дробь, умножьте обе части на [latex]n[/ латекс]:

[латекс](n)h=\dfrac{2m}{n}(n)[/latex]

Это оставляет:

[латекс]nh=2m[/латекс]

Разделить обе части на 2:

[латекс]\dfrac{nh}{2}=\dfrac{2m}{2}[/latex]

Что уменьшает до:

[латекс]м=\dfrac{nh}{2}[/латекс]

Изолировать переменную [latex]b[/latex] в уравнении [latex]A=\dfrac{a}{2-b}. [/latex]

Чтобы очистить дробь, умножьте обе части на [latex]( 2-b)[/latex]:

[латекс](2-b)A=\dfrac{a}{2-b}(2-b)[/latex]

Что сводится к:

[латекс ]А(2-б)=а[/латекс]

Распределите [латекс]А[/латекс] по всему [латексу](2-b),[/латекс], затем изолируйте:

[латекс]\begin{array}{rrrrl} 2A&-&Ab&=&a \\ -2A&&&& \phantom{a}-2A \\ \hline &&-Ab&=&a-2A \end{array}[/latex]

Наконец, разделите обе части на [latex]-A[/latex]:

[latex] \dfrac{-Ab}{-A}=\dfrac{a-2A}{-A}[/latex]

Решение:

[latex]b=\dfrac{a-2A}{-A}\text {или}b=\dfrac{2A-a}{A}[/latex]

В вопросах с 1 по 10 оцените каждое выражение, используя заданные значения. 93\текст{ (}х=5, г=4)[/латекс]

В вопросах с 11 по 34 выделите указанную переменную из уравнения.

  1. [латекс]b\текст{ в }ab=c[/латекс]
  2. [латекс]h\text{ в }g=\dfrac{h}{i}[/latex]
  3. [латекс] х \ текст { в } \ влево (\ dfrac {f} {г} \ вправо) х = б [/ латекс]
  4. [латекс]y\text{ в }p=\dfrac{3y}{q}[/latex]
  5. [латекс]x\текст{ в }3x=\dfrac{a}{b}[/latex]
  6. [латекс]у\текст{ в}\dfrac{ym}{b}=\dfrac{c}{d}[/latex]
  7. [латекс]\pi\text{ в }V=\dfrac{4}{3}\pi r^3[/latex] 92[/латекс]
  8. [латекс]y\текст{ в }c=\dfrac{4y}{m+n}[/latex]
  9. [латекс]r\текст{ в}\dfrac{rs}{a-3}=k[/латекс]
  10. [латекс]D\текст{in}V=\dfrac{\pi Dn}{12}[/латекс]
  11. [латекс]R\текст{ в }F=k(R-L)[/латекс]
  12. [латекс]с\текст{ в }P=n(pc)[/латекс]
  13. [латекс]L\текст{ в }S=L+2B[/латекс]
  14. [латекс]D\текст{ в }T=\dfrac{D-d}{L}[/латекс]
  15. [латекс]E_a\текст{ в }I=\dfrac{E_a-E_q}{R}[/латекс]
  16. [латекс]L_o\текст{ в }L=L_o(1+at)[/латекс]
  17. [латекс]м\текст{ в }2м+р=4м+q[/латекс]
  18. [латекс]k\text{ в }\dfrac{km}{r}=q[/латекс]
  19. [латекс]Т\текст{ в }R=aT+b[/латекс]
  20. [латекс]Q_2\текст{ в }Q_1=P(Q_2-Q_1)[/латекс]
  21. [латекс]r_1\текст{ в }L=\pi(r_1+r_2)+2d[/латекс]
  22. [латекс]T_1\текст{ в}R=\dfrac{kA(T+T_1)}{d}[/латекс]
  23. [латекс]V_2\текст{ в }P=\dfrac{V_1(V_2-V_1)}{г}[/латекс]

Ключ ответа 2. 6

Решение переменной и работа с формулами | Алгебра 1 | Решение линейных уравнений

Дополнительные темы

по нахождению переменной и работе с формулами

Популярные учебные пособия

по нахождению переменной и работе с формулами

    Как решить формулу для переменной?

    Итак, вы решаете математическую задачу и у вас есть правильная формула. Большой! Но переменная, которую нужно найти, не входит в формулу сама по себе. Не так здорово. Не волнуйся! В этом уроке вы узнаете, как решить формулу для нужной переменной!

    Что такое буквальное уравнение?

    Буквенное уравнение — это уравнение, в котором переменные представляют известные значения. Буквенные уравнения позволяют использовать для представления такие вещи, как расстояние, время, проценты и наклон, как переменные в уравнении. Использование переменных вместо слов реально экономит время! Узнайте о буквальных уравнениях с помощью этого урока.

    Как найти переменную через другую переменную?

    Есть уравнение с двумя переменными? Хотите решить для одной переменной с точки зрения другой? Хотите пойти наоборот? Посмотрите, как в этом уроке!

    Как найти длину прямоугольника, если известны его ширина и площадь?

    Как найти длину прямоугольника, если известны ширина и площадь? Этот урок покажет вам, как!

    Как использовать решение уравнения для вычисления выражения?

    Если 3x=21, чему равно 9x? Чтобы получить ответ, решите уравнение относительно переменной. Затем подставьте это значение переменной в выражение и упростите, чтобы получить ответ. Следуйте этому же процессу в любое время, когда вам нужно использовать уравнение для вычисления выражения. Посмотрите этот урок, чтобы увидеть этот процесс в действии!

    Как использовать формулу простых процентов?

    Если у вас уже есть банковский счет или вы планируете открыть его в будущем, вам обязательно нужно ознакомиться с этим руководством! Следите за тем, как в этом учебнике рассматривается задача со словами, включающая простые проценты.

    Что такое формула простых процентов?

    Проценты можно найти во многих местах: сберегательные счета, ипотечные кредиты, кредиты, инвестиции, кредитные карты и многое другое! Посмотрите этот урок и узнайте, как рассчитать простые проценты!

    Как решить более сложную задачу с процентами?

    Ищете инвестиции? Вы уже инвестируете? Тогда этот урок обязателен к просмотру! Следите за тем, как в этом учебнике рассматривается задача со словами, включающая простые проценты.

    Как рассчитать пройденное время, если известны расстояние и скорость?

    В этом учебном пособии представлено отличное практическое применение математики. Вы увидите, как использовать равномерное движение, чтобы вычислить, сколько времени потребуется, чтобы пройти определенное расстояние с постоянной скоростью. Проверьте это!

    Какая формула связывает расстояние, скорость и время?

    Когда у вас есть постоянная скорость, одна и та же формула появляется снова и снова, и это формула, которая связывает расстояние, скорость и время.

Читайте также: