Формулы для работы: Механическая работа — урок. Физика, 9 класс.
Содержание
Формула работы
- Евсиевич Нинель Валерьевна
Разделы:
Начальная школа
Цели:
- сформировать представление о величине
«производительность», выявить зависимость между
величинами: объем выполненной работы (А),
производительность (V) и время (t), построить
формулу работы А = V * t, V = A : t, t = A : V. - повторить и закрепить решение примеров на
порядок действий, соотношение между единицами
дины, времени, массы.
ХОД УРОКА
I.
– Кто из Вас знает, кем работают ваши родители и
на каком предприятии они трудятся?
– А кто из Вас знает пословицы о труде?
- Работа силушку копит, а лень ее топит.

- Под лежачий камень вода не течет.
- Трудолюбив, как муравей.
- Не спеши языком, торопись делом.
- Кто мало говорит, тот много делает.
- Без труда не вытащишь рыбку из пруда.
- Рабочие руки не знают скуки.
- Дело мастера боится.
- Всякое умение трудом дается.
- Без труда нет добра.
- Без труда день годом станет.
- Горька работа, да сладок мед.
II. Актуализация знаний
(На доске таблица и формулы. Дети придумывают
задачи и решают устно)
| S | V | t |
| ? км | 60 км/ч | 4 ч |
| 720 км | ? км/ч | 6 ч |
| 57 км | 19 км/ч | ? ч |
– Найдите среди формул те, которые показывают,
как найти неизвестные значения пути, скорости и
времени. (Формулы выставляются на доске и
(Формулы выставляются на доске и
комментируются)
– А зачем вообще нужны формулы? (Показывают,
как решать похожие между собой задачи).
– Подберите формулы для решения первой задачи.
(S = V * t)
– Придумайте по этой формуле задачу, аналогичную
первой задачи.
– Запишите формулу, подходящую к задаче: «Один
всадник проскакал 70 км за 2 ч, а второй – 90 км за 3
ч. Какой из них скакал быстрее?» (V = S: t)
– Решите эту задачу, пользуясь формулой.
(1. 70 : 2 = 35 (км/ч) – скорость первого всадника.
2. 90 : 3 = 30 (км/ч) – скорость второго всадника.
3. 35 км/ч > 30 км/ч => 1 всадник скакал быстрее)
III. Постановка проблемы
– Подберите формулу к задаче: «Один мастер
сделал 2 детали за 4 часа, а второй – 21 деталь
за 3 часа. Кто из них работал быстрее?» (Подходящей
формулы среди данных нет)
– Сформулируйте цель урока –
установить, какие величины описывают процесс
выполнения работы, и установить взаимосвязь
между ними.
– Тема урока – Формула работы.
IV. «Открытие» детьми нового знания.
– О каких величинах идет речь в последней
задаче – о площади, объеме, пройденном пути? (Нет.
В задаче говориться о количестве деталей,
сделанных рабочими, о скорости и времени их
работы).
– Как найти скорость работы мастеров? (Надо
количество сделанных деталей разделить на время
работы).
– Скорость работы называют производительностью
и обозначают (V), всю выполненную работу – А, время
работы – t.
– Попробуйте установить взаимосвязь между этими
величинами. (А = V * t, V = A : t, t = A : V)
– Теперь, зная формулу работы, давайте решим
задачу.
V = A : t
1. 24 : 4 = 6 (дет./ч) – производительность первого
мастера.
2. 21 : 3 = 7 (дет./ч) – производительность второго
мастера.
3. Второй мастер работал быстрее.
Практическая работа на производительность
– Решите устно в течение 2 минут следующие
уравнения.
9 + х =
12
х – 27 =
8 5
* х = 25
8 * х =
480
52 : х =
13 420
: х = 7
40 – х =
12
х : 19 =
4 800
+ х = 823
90 : х =
5
34 – х =
17 х
– 36 = 15
х * 50 = 250
18 + х =
110 х
– 25 = 118
– Давайте проверим количество правильных
ответов и вычислим производительность каждого
из вас.
– Как это сделать? (Количество верных ответов
разделить на 2).
– А какая у вас производительность за урок? (То
что получилось умножить на 45 минут).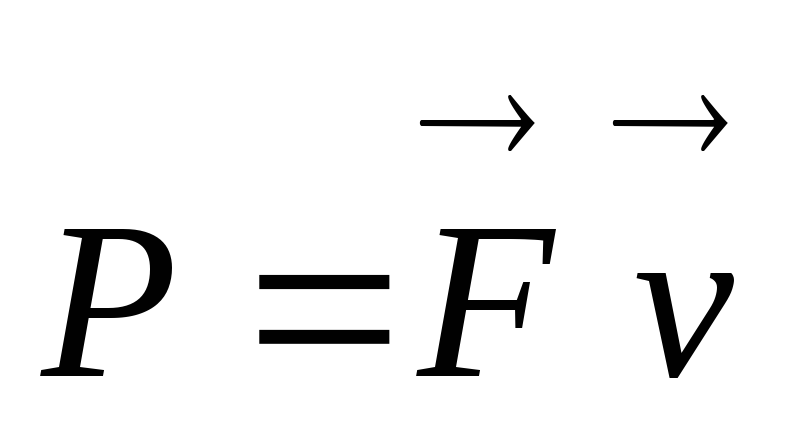
Закрепление понятия «производительность»
- С. 44, №1
V. Первичное закрепление
- С.44, №2
- С. 44, №3
- С.44, №4 (а)
VI. Самостоятельная работа с самопроверкой
по эталону
- С.44, №4 (б).
VII. Закрепление пройденного
- С.45, №10 (а)
VIII. Итог
– Что сегодня на уроке было самым интересным?
– Что сегодня на уроке было главным?
– Где нам могут пригодиться эти знания?
– Какую поговорку выберем своим девизом?
IX. Домашнее задание
- С.44, №5 и №7
Приложение 1
Работа, мощность, энергия — Физика — Теория, тесты, формулы и задачи
Оглавление:
- Основные теоретические сведения
- Механическая работа
- Мощность
- Кинетическая энергия
- Потенциальная энергия
- Коэффициент полезного действия
- Закон сохранения механической энергии
- Некоторые рекомендации к решению задач на работу
- Закон сохранения энергии и динамика вращательного движения
- Неупругие соударения
- Абсолютно упругий удар
- Рекомендации к решению некоторых сложных задач на законы сохранения
Механическая работа
К оглавлению. ..
..
Энергетические характеристики движения вводятся на основе понятия механической работы или работы силы. Работой, совершаемой постоянной силой F, называется физическая величина, равная произведению модулей силы и перемещения, умноженному на косинус угла между векторами силы F и перемещения S:
Работа является скалярной величиной. Она может быть как положительна (0° ≤ α < 90°), так и отрицательна (90° < α ≤ 180°). При α = 90° работа, совершаемая силой, равна нулю. В системе СИ работа измеряется в джоулях (Дж). Джоуль равен работе, совершаемой силой в 1 ньютон на перемещении 1 метр в направлении действия силы.
Если же сила изменяется с течением времени, то для нахождения работы строят график зависимости силы от перемещения и находят площадь фигуры под графиком – это и есть работа:
Примером силы, модуль которой зависит от координаты (перемещения), может служить сила упругости пружины, подчиняющаяся закону Гука (Fупр = kx).
Мощность
К оглавлению…
Работа силы, совершаемая в единицу времени, называется мощностью. Мощность P (иногда обозначают буквой N) – физическая величина, равная отношению работы A к промежутку времени t, в течение которого совершена эта работа:
По этой формуле рассчитывается средняя мощность, т.е. мощность обобщенно характеризующая процесс. Итак, работу можно выражать и через мощность: A = Pt (если конечно известна мощность и время совершения работы). Единица мощности называется ватт (Вт) или 1 джоуль за 1 секунду. Если движение равномерное, то:
По этой формуле мы можем рассчитать мгновенную мощность (мощность в данный момент времени), если вместо скорости подставим в формулу значение мгновенной скорости. Как узнать, какую мощность считать? Если в задаче спрашивают мощность в момент времени или в какой-то точке пространства, то считается мгновенная. Если спрашивают про мощность за какой-то промежуток времени или участок пути, то ищите среднюю мощность.
Если спрашивают про мощность за какой-то промежуток времени или участок пути, то ищите среднюю мощность.
КПД – коэффициент полезного действия, равен отношению полезной работы к затраченной, либо же полезной мощности к затраченной:
Какая работа полезная, а какая затраченная определяется из условия конкретной задачи путем логического рассуждения. К примеру, если подъемный кран совершает работу по подъему груза на некоторую высоту, то полезной будет работа по поднятию груза (так как именно ради нее создан кран), а затраченной – работа, совершенная электродвигателем крана.
Итак, полезная и затраченная мощность не имеют строгого определения, и находятся логическим рассуждением. В каждой задаче мы сами должны определить, что в этой задаче было целью совершения работы (полезная работа или мощность), а что было механизмом или способом совершения всей работы (затраченная мощность или работа).
В общем случае КПД показывает, как эффективно механизм преобразует один вид энергии в другой. Если мощность со временем изменяется, то работу находят как площадь фигуры под графиком зависимости мощности от времени:
Если мощность со временем изменяется, то работу находят как площадь фигуры под графиком зависимости мощности от времени:
Кинетическая энергия
К оглавлению…
Физическая величина, равная половине произведения массы тела на квадрат его скорости, называется кинетической энергией тела (энергией движения):
То есть если автомобиль массой 2000 кг движется со скоростью 10 м/с, то он обладает кинетической энергией равной Ек = 100 кДж и способен совершить работу в 100 кДж. Эта энергия может превратиться в тепловую (при торможении автомобиля нагревается резина колес, дорога и тормозные диски) или может быть потрачена на деформацию автомобиля и тела, с которым автомобиль столкнулся (при аварии). При вычислении кинетической энергии не имеет значения куда движется автомобиль, так как энергия, как и работа, величина скалярная.
Тело обладает энергией, если способно совершить работу. Например, движущееся тело обладает кинетической энергией, т. е. энергией движения, и способно совершать работу по деформации тел или придания ускорения телам, с которыми произойдёт столкновение.
е. энергией движения, и способно совершать работу по деформации тел или придания ускорения телам, с которыми произойдёт столкновение.
Физический смысл кинетической энергии: для того чтобы покоящееся тело массой m стало двигаться со скоростью v необходимо совершить работу равную полученному значению кинетической энергии. Если тело массой m движется со скоростью v, то для его остановки необходимо совершить работу равную его первоначальной кинетической энергии. При торможении кинетическая энергия в основном (кроме случаев соударения, когда энергия идет на деформации) «забирается» силой трения.
Теорема о кинетической энергии: работа равнодействующей силы равна изменению кинетической энергии тела:
Теорема о кинетической энергии справедлива и в общем случае, когда тело движется под действием изменяющейся силы, направление которой не совпадает с направлением перемещения. Применять данную теорему удобно в задачах на разгон и торможение тела.
Потенциальная энергия
К оглавлению…
Наряду с кинетической энергией или энергией движения в физике важную роль играет понятие потенциальной энергии или энергии взаимодействия тел.
Потенциальная энергия определяется взаимным положением тел (например, положением тела относительно поверхности Земли). Понятие потенциальной энергии можно ввести только для сил, работа которых не зависит от траектории движения тела и определяется только начальным и конечным положениями (так называемые консервативные силы). Работа таких сил на замкнутой траектории равна нулю. Таким свойством обладают сила тяжести и сила упругости. Для этих сил можно ввести понятие потенциальной энергии.
Потенциальная энергия тела в поле силы тяжести Земли рассчитывается по формуле:
Физический смысл потенциальной энергии тела: потенциальная энергия равна работе, которую совершает сила тяжести при опускании тела на нулевой уровень (h – расстояние от центра тяжести тела до нулевого уровня). Если тело обладает потенциальной энергией, значит оно способно совершить работу при падении этого тела с высоты h до нулевого уровня. Работа силы тяжести равна изменению потенциальной энергии тела, взятому с противоположным знаком:
Если тело обладает потенциальной энергией, значит оно способно совершить работу при падении этого тела с высоты h до нулевого уровня. Работа силы тяжести равна изменению потенциальной энергии тела, взятому с противоположным знаком:
Часто в задачах на энергию приходится находить работу по поднятию (переворачиванию, доставанию из ямы) тела. Во всех этих случаях нужно рассматривать перемещение не самого тела, а только его центра тяжести.
Потенциальная энергия Ep зависит от выбора нулевого уровня, то есть от выбора начала координат оси OY. В каждой задаче нулевой уровень выбирается из соображения удобства. Физический смысл имеет не сама потенциальная энергия, а ее изменение при перемещении тела из одного положения в другое. Это изменение не зависит от выбора нулевого уровня.
Потенциальная энергия растянутой пружины рассчитывается по формуле:
где: k – жесткость пружины. Растянутая (или сжатая) пружина способна привести в движение прикрепленное к ней тело, то есть сообщить этому телу кинетическую энергию. Следовательно, такая пружина обладает запасом энергии. Растяжение или сжатие х надо рассчитывать от недеформированного состояния тела.
Следовательно, такая пружина обладает запасом энергии. Растяжение или сжатие х надо рассчитывать от недеформированного состояния тела.
Потенциальная энергия упруго деформированного тела равна работе силы упругости при переходе из данного состояния в состояние с нулевой деформацией. Если в начальном состоянии пружина уже была деформирована, а ее удлинение было равно x1, тогда при переходе в новое состояние с удлинением x2 сила упругости совершит работу, равную изменению потенциальной энергии, взятому с противоположным знаком (так как сила упругости всегда направлена против деформации тела):
Потенциальная энергия при упругой деформации – это энергия взаимодействия отдельных частей тела между собой силами упругости.
Работа силы трения зависит от пройденного пути (такой вид сил, чья работа зависит от траектории и пройденного пути называется: диссипативные силы). Понятие потенциальной энергии для силы трения вводить нельзя.
Коэффициент полезного действия
К оглавлению…
Коэффициент полезного действия (КПД) – характеристика эффективности системы (устройства, машины) в отношении преобразования или передачи энергии. Он определяется отношением полезно использованной энергии к суммарному количеству энергии, полученному системой (формула уже приведена выше).
КПД можно рассчитывать как через работу, так и через мощность. Полезная и затраченная работа (мощность) всегда определяются путем простых логических рассуждений.
В электрических двигателях КПД – отношение совершаемой (полезной) механической работы к электрической энергии, получаемой от источника. В тепловых двигателях – отношение полезной механической работы к затрачиваемому количеству теплоты. В электрических трансформаторах – отношение электромагнитной энергии, получаемой во вторичной обмотке, к энергии, потребляемой первичной обмоткой.
В силу своей общности понятие КПД позволяет сравнивать и оценивать с единой точки зрения такие различные системы, как атомные реакторы, электрические генераторы и двигатели, теплоэнергетические установки, полупроводниковые приборы, биологические объекты и т. д.
д.
Из–за неизбежных потерь энергии на трение, на нагревание окружающих тел и т.п. КПД всегда меньше единицы. Соответственно этому КПД выражается в долях затрачиваемой энергии, то есть в виде правильной дроби или в процентах, и является безразмерной величиной. КПД характеризует как эффективно работает машина или механизм. КПД тепловых электростанций достигает 35–40%, двигателей внутреннего сгорания с наддувом и предварительным охлаждением – 40–50%, динамомашин и генераторов большой мощности – 95%, трансформаторов – 98%.
Задачу, в которой нужно найти КПД или он известен, надо начать с логического рассуждения – какая работа является полезной, а какая затраченной.
Закон сохранения механической энергии
К оглавлению…
Полной механической энергией называется сумма кинетической энергии (т.е. энергии движения) и потенциальной (т.е. энергии взаимодействия тел силами тяготения и упругости):
Если механическая энергия не переходит в другие формы, например, во внутреннюю (тепловую) энергию, то сумма кинетической и потенциальной энергии остаётся неизменной. Если же механическая энергия переходит в тепловую, то изменение механической энергии равно работе силы трения или потерям энергии, или количеству выделившегося тепла и так далее, другими словами изменение полной механической энергии равно работе внешних сил:
Если же механическая энергия переходит в тепловую, то изменение механической энергии равно работе силы трения или потерям энергии, или количеству выделившегося тепла и так далее, другими словами изменение полной механической энергии равно работе внешних сил:
Сумма кинетической и потенциальной энергии тел, составляющих замкнутую систему (т.е. такую в которой не действует внешних сил, и их работа соответственно равна нолю) и взаимодействующих между собой силами тяготения и силами упругости, остается неизменной:
Это утверждение выражает закон сохранения энергии (ЗСЭ) в механических процессах. Он является следствием законов Ньютона. Закон сохранения механической энергии выполняется только тогда, когда тела в замкнутой системе взаимодействуют между собой силами упругости и тяготения. Во всех задачах на закон сохранения энергии всегда будет как минимум два состояния системы тел. Закон гласит, что суммарная энергия первого состояния будет равна суммарной энергии второго состояния.
Алгоритм решения задач на закон сохранения энергии:
- Найти точки начального и конечного положения тела.
- Записать какой или какими энергиями обладает тело в данных точках.
- Приравнять начальную и конечную энергию тела.
- Добавить другие необходимые уравнения из предыдущих тем по физике.
- Решить полученное уравнение или систему уравнений математическими методами.
Важно отметить, что закон сохранения механической энергии позволил получить связь между координатами и скоростями тела в двух разных точках траектории без анализа закона движения тела во всех промежуточных точках. Применение закона сохранения механической энергии может в значительной степени упростить решение многих задач.
В реальных условиях практически всегда на движущиеся тела наряду с силами тяготения, силами упругости и другими силами действуют силы трения или силы сопротивления среды. Работа силы трения зависит от длины пути.
Если между телами, составляющими замкнутую систему, действуют силы трения, то механическая энергия не сохраняется. Часть механической энергии превращается во внутреннюю энергию тел (нагревание). Таким образом энергия в целом (т.е. не только механическая) в любом случае сохраняется.
При любых физических взаимодействиях энергия не возникает и не исчезает. Она лишь превращается из одной формы в другую. Этот экспериментально установленный факт выражает фундаментальный закон природы – закон сохранения и превращения энергии.
Одним из следствий закона сохранения и превращения энергии является утверждение о невозможности создания «вечного двигателя» (perpetuum mobile) – машины, которая могла бы неопределенно долго совершать работу, не расходуя при этом энергии.
Разные задачи на работу
К оглавлению…
Если в задаче требуется найти механическую работу, то сначала выберите способ её нахождения:
- Работу можно найти по формуле: A = FS∙cosα.
 Найдите силу, совершающую работу, и величину перемещения тела под действием этой силы в выбранной системе отсчёта. Обратите внимание, что угол должен быть выбран между векторами силы и перемещения.
Найдите силу, совершающую работу, и величину перемещения тела под действием этой силы в выбранной системе отсчёта. Обратите внимание, что угол должен быть выбран между векторами силы и перемещения. - Работу внешней силы можно найти, как разность механической энергии в конечной и начальной ситуациях. Механическая энергия равна сумме кинетической и потенциальной энергий тела.
- Работу по подъёму тела с постоянной скоростью можно найти по формуле: A = mgh, где h – высота, на которую поднимается центр тяжести тела.
- Работу можно найти как произведение мощности на время, т.е. по формуле: A = Pt.
- Работу можно найти, как площадь фигуры под графиком зависимости силы от перемещения или мощности от времени.
Закон сохранения энергии и динамика вращательного движения
К оглавлению…
Задачи этой темы являются достаточно сложными математически, но при знании подхода решаются по совершенно стандартному алгоритму. Во всех задачах Вам придется рассматривать вращение тела в вертикальной плоскости. Решение будет сводиться к следующей последовательности действий:
Во всех задачах Вам придется рассматривать вращение тела в вертикальной плоскости. Решение будет сводиться к следующей последовательности действий:
- Надо определить интересующую Вас точку (ту точку, в которой необходимо определить скорость тела, силу натяжения нити, вес и так далее).
- Записать в этой точке второй закон Ньютона, учитывая, что тело вращается, то есть у него есть центростремительное ускорение.
- Записать закон сохранения механической энергии так, чтобы в нем присутствовала скорость тела в той самой интересной точке, а также характеристики состояния тела в каком-нибудь состоянии про которое что-то известно.
- В зависимости от условия выразить скорость в квадрате из одного уравнения и подставить в другое.
- Провести остальные необходимые математические операции для получения окончательного результата.
При решении задач надо помнить, что:
- Условие прохождения верхней точки при вращении на нити с минимальной скоростью – сила реакции опоры N в верхней точке равна 0.
 Такое же условие выполняется при прохождении верхней точки мертвой петли.
Такое же условие выполняется при прохождении верхней точки мертвой петли. - При вращении на стержне условие прохождения всей окружности: минимальная скорость в верхней точке равна 0.
- Условие отрыва тела от поверхности сферы – сила реакции опоры в точке отрыва равна нулю.
Неупругие соударения
К оглавлению…
Закон сохранения механической энергии и закон сохранения импульса позволяют находить решения механических задач в тех случаях, когда неизвестны действующие силы. Примером такого рода задач является ударное взаимодействие тел.
Ударом (или столкновением) принято называть кратковременное взаимодействие тел, в результате которого их скорости испытывают значительные изменения. Во время столкновения тел между ними действуют кратковременные ударные силы, величина которых, как правило, неизвестна. Поэтому нельзя рассматривать ударное взаимодействие непосредственно с помощью законов Ньютона. Применение законов сохранения энергии и импульса во многих случаях позволяет исключить из рассмотрения сам процесс столкновения и получить связь между скоростями тел до и после столкновения, минуя все промежуточные значения этих величин.
С ударным взаимодействием тел нередко приходится иметь дело в обыденной жизни, в технике и в физике (особенно в физике атома и элементарных частиц). В механике часто используются две модели ударного взаимодействия – абсолютно упругий и абсолютно неупругий удары.
Абсолютно неупругим ударом называют такое ударное взаимодействие, при котором тела соединяются (слипаются) друг с другом и движутся дальше как одно тело.
При абсолютно неупругом ударе механическая энергия не сохраняется. Она частично или полностью переходит во внутреннюю энергию тел (нагревание). Для описания любых ударов Вам нужно записать и закон сохранения импульса, и закон сохранения механической энергии с учетом выделяющейся теплоты (предварительно крайне желательно сделать рисунок).
Абсолютно упругий удар
К оглавлению…
Абсолютно упругим ударом называется столкновение, при котором сохраняется механическая энергия системы тел. Во многих случаях столкновения атомов, молекул и элементарных частиц подчиняются законам абсолютно упругого удара. При абсолютно упругом ударе наряду с законом сохранения импульса выполняется закон сохранения механической энергии. Простым примером абсолютно упругого столкновения может быть центральный удар двух бильярдных шаров, один из которых до столкновения находился в состоянии покоя.
Во многих случаях столкновения атомов, молекул и элементарных частиц подчиняются законам абсолютно упругого удара. При абсолютно упругом ударе наряду с законом сохранения импульса выполняется закон сохранения механической энергии. Простым примером абсолютно упругого столкновения может быть центральный удар двух бильярдных шаров, один из которых до столкновения находился в состоянии покоя.
Центральным ударом шаров называют соударение, при котором скорости шаров до и после удара направлены по линии центров. Таким образом, пользуясь законами сохранения механической энергии и импульса, можно определить скорости шаров после столкновения, если известны их скорости до столкновения. Центральный удар очень редко реализуется на практике, особенно если речь идет о столкновениях атомов или молекул. При нецентральном упругом соударении скорости частиц (шаров) до и после столкновения не направлены по одной прямой.
Частным случаем нецентрального упругого удара может служить соударения двух бильярдных шаров одинаковой массы, один из которых до соударения был неподвижен, а скорость второго была направлена не по линии центров шаров. В этом случае векторы скоростей шаров после упругого соударения всегда направлены перпендикулярно друг к другу.
В этом случае векторы скоростей шаров после упругого соударения всегда направлены перпендикулярно друг к другу.
Законы сохранения. Сложные задачи
К оглавлению…
Несколько тел
В некоторых задачах на закон сохранения энергии тросы с помощью которых перемещаются некие объекты могут иметь массу (т.е. не быть невесомыми, как Вы могли уже привыкнуть). В этом случае работу по перемещению таких тросов (а именно их центров тяжести) также нужно учитывать.
Если два тела, соединённые невесомым стержнем, вращаются в вертикальной плоскости, то:
- выбирают нулевой уровень для расчёта потенциальной энергии, например на уровне оси вращения или на уровне самой нижней точки нахождения одного из грузов и обязательно делают чертёж;
- записывают закон сохранения механической энергии, в котором в левой части записывают сумму кинетической и потенциальной энергии обоих тел в начальной ситуации, а в правой части записывают сумму кинетической и потенциальной энергии обоих тел в конечной ситуации;
- учитывают, что угловые скорости тел одинаковы, тогда линейные скорости тел пропорциональны радиусам вращения;
- при необходимости записывают второй закон Ньютона для каждого из тел в отдельности.

Разрыв снаряда
В случае разрыва снаряда выделяется энергия взрывчатых веществ. Чтобы найти эту энергию надо от суммы механических энергий осколков после взрыва отнять механическую энергию снаряда до взрыва. Также будем использовать закон сохранения импульса, записанный, в виде теоремы косинусов (векторный метод) или в виде проекций на выбранные оси.
Столкновения с тяжёлой плитой
Пусть навстречу тяжёлой плите, которая движется со скоростью v, движется лёгкий шарик массой m со скоростью uн. Так как импульс шарика много меньше импульса плиты, то после удара скорость плиты не изменится, и она будет продолжать движение с той же скоростью и в том же направлении. В результате упругого удара, шарик отлетит от плиты. Здесь важно понять, что не поменяется скорость шарика относительно плиты. В таком случае, для конечной скорости шарика получим:
Таким образом, скорость шарика после удара увеличивается на удвоенную скорость стены. Аналогичное рассуждение для случая, когда до удара шарик и плита двигались в одном направлении, приводит к результату согласно которому скорость шарика уменьшается на удвоенную скорость стены:
Аналогичное рассуждение для случая, когда до удара шарик и плита двигались в одном направлении, приводит к результату согласно которому скорость шарика уменьшается на удвоенную скорость стены:
Задачи о максимальных и минимальных значениях энергии сталкивающихся шаров
В задачах такого типа главное понять, что потенциальная энергия упругой деформации шаров максимальна, если кинетическая энергия их движения минимальна – это следует из закона сохранения механической энергии. Сумма кинетических энергий шаров минимальна в тот момент, когда скорости шаров будут одинаковы по величине и направлены в одном направлении. В этот момент относительная скорость шаров равна нулю, а деформация и связанная с ней потенциальная энергия максимальна.
Формула работы: физическое уравнение с примерами
В физике говорят, что сила совершает работу , если приложение силы смещает объект в направлении действия силы. Другими словами, работа эквивалентна приложению силы на расстоянии.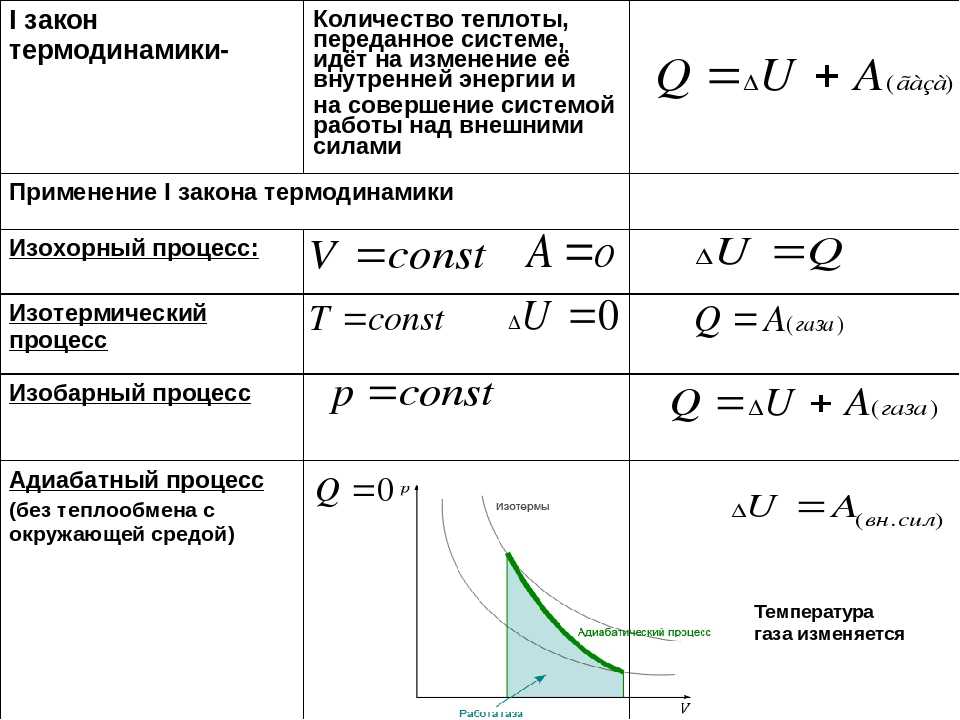 Объем работы, которую совершает сила, прямо пропорционален тому, насколько далеко эта сила перемещает объект. Общая формула для работы и для определения количества работы, выполненной над объектом:
Объем работы, которую совершает сила, прямо пропорционален тому, насколько далеко эта сила перемещает объект. Общая формула для работы и для определения количества работы, выполненной над объектом:
- Вт = F × D × cos(Θ)
где Вт — количество работы, F — вектор силы,
4 D — величина перемещения, угол между вектором силы и вектором смещения. Единицей работы в системе СИ является
джоуля ( Дж ), а его размеры равны кг•м 2 /с 2 . Другой способ понять это состоит в том, что один джоуль эквивалентен количеству энергии, передаваемой, когда сила в один ньютон перемещает объект на расстояние в один метр.
Формула работы
Всякий раз, когда сила перемещает объект, мы говорим, что работа выполнена. Когда мяч скатывается с холма под действием силы тяжести, когда вы поднимаете свой рюкзак с земли, когда внутренний двигатель вашего автомобиля прикладывает силу, заставляющую ваши колеса двигаться; все эти события связаны с силой, перемещающей объект на расстояние, и поэтому требуют некоторой работы. В тех случаях, когда к объекту приложена сила, но он не перемещается, работа не совершается. Таким образом, сила человека, толкающего стену небоскреба, не совершает никакой работы, поскольку небоскреб не движется. Рассмотрим несколько простых примеров, иллюстрирующих понятие работы.
В тех случаях, когда к объекту приложена сила, но он не перемещается, работа не совершается. Таким образом, сила человека, толкающего стену небоскреба, не совершает никакой работы, поскольку небоскреб не движется. Рассмотрим несколько простых примеров, иллюстрирующих понятие работы.
Примеры задач
(1)
К ящику массой 15 кг в горизонтальном направлении приложена сила в 100 ньютонов, которая перемещает его на 5 метров по горизонтали. Сколько работы было сделано?
В этом случае мы знаем, что сила равна 100 Н, а расстояние – 5 метров. Мы также знаем, что, поскольку сила приложена в том же направлении, что и смещение, Θ равно 0. Таким образом, мы подставляем эти значения в наше уравнение
и получим:
- Вт = 100(5)cos(0)= 500 Дж
Итак, сила в 100 Н совершила 500 джоулей 5 метров 5 900 900 перемещения блока.
(2)
На столе лежит двухкилограммовая книга. К книге приложена сила 64 Н под углом 120° к горизонтали, которая перемещает книгу на 3 м в горизонтальном направлении. Сколько работы было сделано?
Сколько работы было сделано?
В данном случае мы знаем силу 64 Н и расстояние 3 м. Мы также знаем, что между углом направления приложенной силы и направлением движения существует угол 120°. Таким образом, подставив эти значения в наше удобное уравнение, мы получим:
- Вт = 64(3)cos(120)= 156,32 Дж
Итак, сила 64 Н под углом 120° выполнила 156,32 м3 0 90 джоулей работы по перемещению книги 9000.
(3)
Линда поднимает чемодан с усилием 300 Н на 3 лестничных пролета на общую высоту 16 метров. Затем она толкает чемодан с силой 100 Н оставшиеся 8 метров до своего гостиничного номера. Сколько работы было сделано за всю ее поездку?
Этот вопрос требует 2 отдельных шагов. Ее поездка состоит из двух основных частей, поэтому мы можем рассчитать работу, проделанную для каждой части отдельно, а затем объединить два значения, чтобы получить общий объем выполненной работы. В первой части своего пути она прикладывает силу 300 Н, чтобы переместить чемодан на 16 метров по вертикали, поэтому количество выполненной работы равно:
- Вт 1 = 300(16)cos(0)= 4800 Дж
Таким образом, в первой части пути было потрачено 4800 Дж. Что касается второй части, мы знаем, что сила в 100 Н переместила чемодан по горизонтали на 8 метров, поэтому общая работа, выполненная на втором участке пути, равна:
Что касается второй части, мы знаем, что сила в 100 Н переместила чемодан по горизонтали на 8 метров, поэтому общая работа, выполненная на втором участке пути, равна:
- Вт 2 =100(8)cos(0) = 800 Дж
Объединение двух значений каждой части пути дает:
- Вт Всего = W 1 + W 2 = 4800 + 800 = 5600 Joules
, так что на протяжении всего курса Trip Linda 5600 Joules из работы.
Отношение работы/энергии
Три основных уравнения, представляющие отношения между энергией, работой и силой.
Работа и энергия в физике тесно связаны. В соответствии с принципом работы-энергии увеличение кинетической энергии твердого тела вызывается равной работой, совершаемой над этим телом силой, приложенной к этому телу. В более математических терминах отношение можно выразить следующим образом:
- W = KE окончательная −KE начальная
, где KE означает кинетическую энергию. Другими словами, изменение кинетической энергии тела равно работе, совершенной над этим телом. В общем, формула для кинетической энергии объекта:
Другими словами, изменение кинетической энергии тела равно работе, совершенной над этим телом. В общем, формула для кинетической энергии объекта:
- KE = (1/2) кг*в 2
, где v обозначает скорость объекта. Единицей кинетической энергии является та же единица работы, что и джоуль. Давайте рассмотрим некоторые задачи, чтобы изучить эти математические отношения.
(4)
Осел и Дидди Конг сидят в 90-килограммовой вагонетке, которая изначально движется горизонтально со скоростью 5 м/с. Носорог Рэмби толкает вагонетку сзади и ускоряет ее, так что теперь она движется со скоростью 11 м/с. Сколько работы Рэмби проделал с вагонеткой?
Чтобы решить эту задачу, нам сначала нужно вычислить начальную кинетическую энергию вагонетки и ее конечную кинетическую энергию. Зная эти значения, мы можем определить общий объем работы. Мы знаем как скорость, так и массу вагонетки, поэтому мы можем определить общую кинетическую энергию в начале и в конце.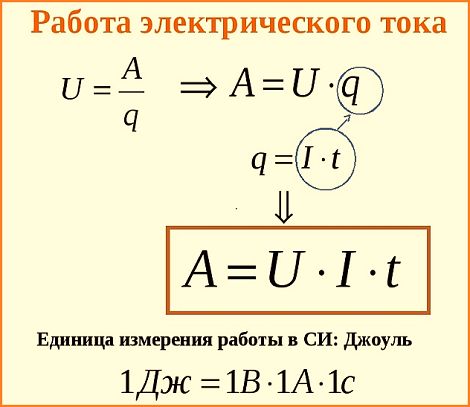 Начальная кинетическая энергия вагонетки:
Начальная кинетическая энергия вагонетки:
- КЭ начальная =(1/2)(90)(5) 2 = 1125 Дж
Конечная кинетическая энергия вагонетки равна 20007/
Таким образом, общая работа, выполненная на вагонетке, равна 5545−1125= 4420 Дж .
«Наука — это знание последствий и зависимости одного факта от другого». – Томас Гоббс
(5)
Автомобиль массой 1300 кг движется со скоростью 18 м/с. Если над автомобилем совершить работу 60000 джоулей, какова будет его конечная скорость?
Вопрос потребует немного алгебры. Во-первых, мы должны определить начальную кинетическую энергию автомобиля. Начальная кинетическая энергия автомобиля равна:
- (1/2)(1300)(18) 2 = 210600 Дж
Так как мы знаем общую работу системы (600000 J) мы можем вычислить конечную кинетическую энергию автомобиля:
- 60000=KE final −210600
- 270600=KE final
Теперь, поскольку мы знаем конечную кинетическую энергию и массу автомобиля, мы можем определить его конечную скорость следующим образом:
8
final =(1/2) kg*v 2
 3 = 2
3 = 2 Конечная скорость автомобиля будет 20,4 м/с .
Таким образом, мы говорим, что работа совершается всякий раз, когда сила перемещает объект на расстояние. Величина работы равна величине силы, умноженной на пройденный путь. Работа и кинетическая энергия тесно взаимосвязаны и могут использоваться для определения друг друга.
Что такое формула работы? Примеры
Формула работы используется для расчета работы. Прежде чем мы выучим формулу, давайте вспомним, что означает работа. Говорят, что работа совершается, когда мы прикладываем силу к объекту, и объект испытывает перемещение. Если перемещение в направлении действия силы равно нулю, то совершенная работа равна нулю. Формула работы используется для расчета работы, совершаемой при перемещении объекта. Давайте узнаем больше о формуле для работы вместе с решенными примерами в следующем разделе.
Что такое формула работы?
Формула работы используется для расчета работы, затраченной на перемещение любого объекта. Работа есть произведение приложенной силы и перемещения в направлении действия силы. Работа есть скалярное произведение двух векторов: силы и перемещения. Таким образом, работа является скалярной величиной. Единицей работы в системе СИ является Джоуль (Дж).
Формула работы
Формула работы может быть выражена следующим образом:
W = F.d
W = (Fcos θ)d
Где,
- W = выполненная работа
- F = Величина приложенной силы
- d = Величина смещения в направлении действия силы.
- θ = угол между векторами: силы и перемещения
Единицей работы в системе СИ является Джоуль (Дж). Если совершена работа в 1 джоуль, то формула для работы будет следующей: 1 Дж = 1 Н·м
Если совершена работа в 1 джоуль, то формула для работы будет следующей: 1 Дж = 1 Н·м
Вывод формулы работы
Рассмотрим блок, помещенный на горизонтальном полу без трения, на который действует постоянная сила F, благодаря которой этот блок перемещается на расстояние d по прямой линии в направлении действия силы.
В общем случае работа силы F равна изменению кинетической энергии 2 -u 2 )
Применение v 2 -u 2 = 2as
W = (1/2)m(2as)
W = maston’s 4 закон), таким образом, W = Fs. (s=d=перемещение)
Теперь, если эффективная составляющая силы вдоль направления перемещения Fcosθ отвечает за перемещение любого объекта в заданном направлении, то работа, совершаемая силой F при перемещении тела на перемещение d есть, W=(|F|cosθ)|d|
Хотите найти сложные математические решения за считанные секунды?
Воспользуйтесь нашим бесплатным онлайн-калькулятором, чтобы решить сложные вопросы. С Cuemath находите решения простыми и легкими шагами.
С Cuemath находите решения простыми и легкими шагами.
Записаться на бесплатный пробный урок
Примеры использования формулы для работы
Пример 1: 10 ньютонов силы, приложенной к телу, которое перемещает его на 2 метра. Вычислите работу, выполненную по формуле работы.
Решение:
Чтобы найти: Работа выполнена
Дано: Сила (F) = 10 Н
Перемещение (d) = 2 м
Используя формулу для работы,
W = F.d
= (10)(2)
= 20 Нм
: 9003 Ответ Работа Нм совершается, когда сила в 10 ньютонов перемещает тело на 2 метра.
Пример 2: Кули на вокзале несет сумку массой 100 Н на некоторое расстояние. Вычислите работу, которую совершает кули над сумкой, используя формулу работы.
Решение:
Найти работу, выполненную кули.
Дано: Вес мешка = 100 Н
Кроме того, вес мешка будет действовать в вертикальном направлении, а его движение будет происходить в горизонтальном направлении. Значит, смещение мешка в направлении действия силы (веса) равно нулю.
Значит, смещение мешка в направлении действия силы (веса) равно нулю.
d = 0
Используя формулу для работы,
W = F.d
= (100)(0)
= 0 Дж
Ответ: Работа, выполненная кули на мешке, равна нулю.
Пример 3: Рассчитайте работу, выполненную силой при перемещении объекта на расстояние 7 м, если объект протаскивается горизонтально по поверхности под действием силы 150 Н, действующей параллельно поверхности.
Решение:
Найти: Работа силы при перемещении тела на расстояние 7 м
Дано: F = 150 Н, d = 7 м
Поскольку F и d направлены в одном направлении,
θ = 0, [θ — угол действия силы к направлению движения]
W = F × Cos θ × d
= 150× 7 × Cos 0
= 1050 Дж [Поскольку Cos 0 = 1]
Ответ: Работа, совершаемая силой при перемещении объекта, равна 800 J.
Часто задаваемые вопросы о формуле работы
Что такое формула работы?
Формула работы определяется как формула для расчета работы, выполненной при перемещении объекта.


 Найдите силу, совершающую работу, и величину перемещения тела под действием этой силы в выбранной системе отсчёта. Обратите внимание, что угол должен быть выбран между векторами силы и перемещения.
Найдите силу, совершающую работу, и величину перемещения тела под действием этой силы в выбранной системе отсчёта. Обратите внимание, что угол должен быть выбран между векторами силы и перемещения.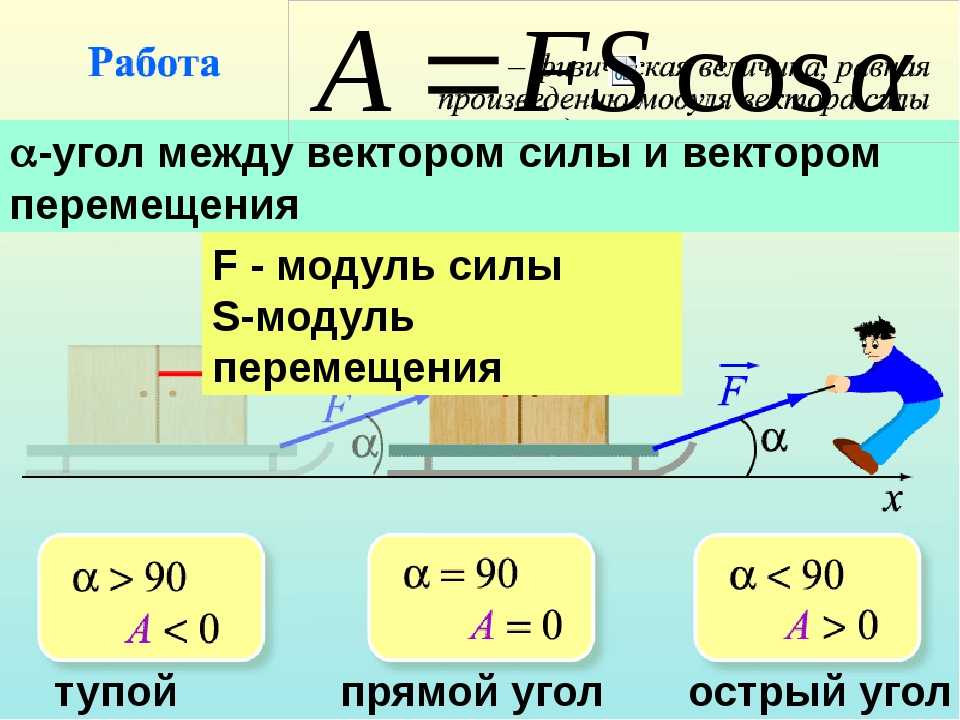 Такое же условие выполняется при прохождении верхней точки мертвой петли.
Такое же условие выполняется при прохождении верхней точки мертвой петли.
