Произведение excel: Функция ПРОИЗВЕД (PRODUCT) — Справочник

Как легко рассчитать скалярный продукт в Excel

В этом руководстве объясняется, как рассчитать скалярный продукт в Excel.

Что такое скалярный продукт?

Для данного вектора a = [a 1 , a 2 , a 3 ] и вектора b = [b 1 , b 2 , b 3 ] скалярное произведение вектора a и вектора b, обозначаемое как a · b , определяется как:

а · b = а 1 * b 1 + а 2 * b 2 + а 3 * b 3

Например, если a = [2, 5, 6] и b = [4, 3, 2], то скалярное произведение a и b будет равно:

а · б = 2*4 + 5*3 + 6*2

а · б = 8 + 15 + 12

а · б = 35

По сути, скалярное произведение — это сумма произведений соответствующих элементов двух векторов.

Как найти точечный продукт в Excel

Чтобы найти скалярное произведение двух векторов в Excel, мы можем использовать следующие шаги:

1. Введите данные.Введите значения данных для каждого вектора в их собственные столбцы. Например, введите значения данных для вектора a = [2, 5, 6] в столбец A и значения данных для вектора b = [4, 3, 2] в столбец B:

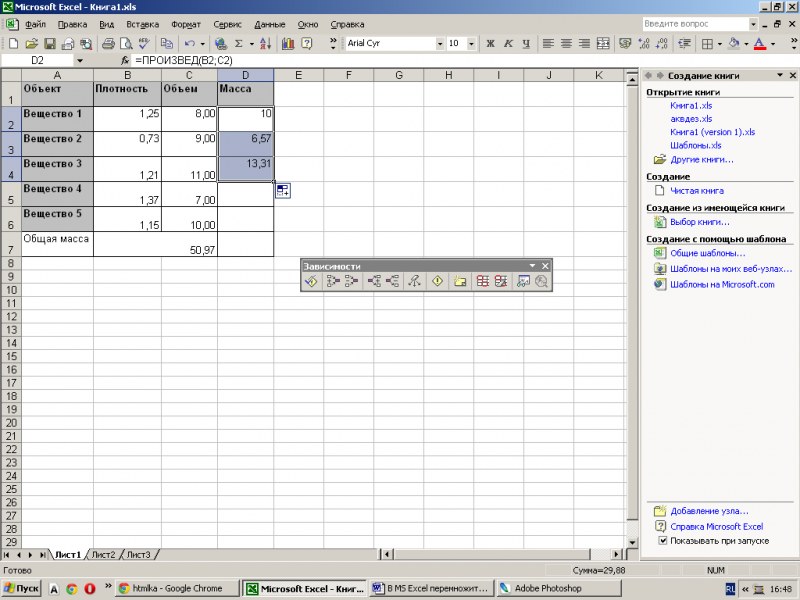
2. Вычислите скалярный продукт. Чтобы вычислить скалярный продукт, мы можем использовать функцию Excel СУММПРОИЗВ() , которая использует следующий синтаксис:

СУММПРОИЗВ(массив1, [массив2], …)

• array — первый массив или диапазон, который необходимо умножить, а затем добавить.
• array2 — второй массив или диапазон для умножения, а затем добавления.

В этом примере мы можем ввести следующее в ячейку D1 , чтобы вычислить скалярное произведение между вектором a и вектором b :

=СУММПРОИЗВ(A1:A3, B1:B3)

Это дает значение 35 , которое соответствует ответу, который мы получили вручную.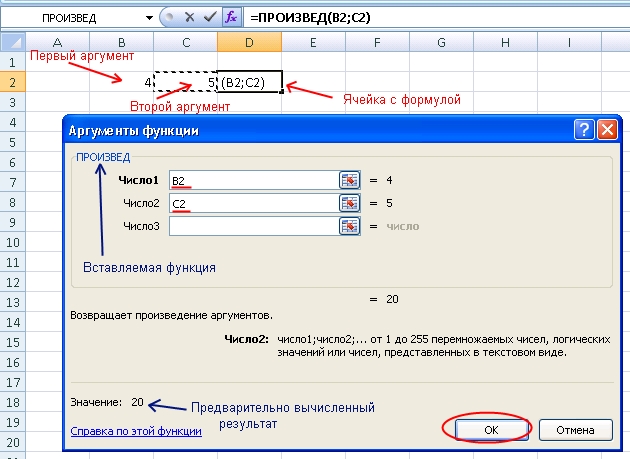

Обратите внимание, что мы можем использовать СУММПРОИЗВ() для нахождения скалярного произведения векторов любой длины. Например, предположим, что вектор a и b имеют длину 20. Затем мы можем ввести следующую формулу в ячейку D1 , чтобы вычислить их скалярное произведение:

=СУММПРОИЗВ(A1:A20, B1:B20)

Возможные ошибки при вычислении скалярного произведения

Функция СУММПРОИЗВ() вернет #ЗНАЧ! ошибка, если векторы не имеют одинаковой длины.

Например, если вектор a имеет длину 20, а вектор b имеет длину 19, то формула =СУММПРОИЗВ(A1:A20, B1:B19) вернет ошибку.

Два вектора должны иметь одинаковую длину, чтобы можно было вычислить скалярное произведение.

Дополнительные ресурсы

В следующих руководствах объясняется, как рассчитать скалярный продукт в различных статистических программах:

Как рассчитать скалярный продукт в Google Sheets
Как рассчитать скалярный продукт в R
Как рассчитать скалярный продукт на калькуляторе TI-84

Векторное произведение в EXCEL.

Примеры и описание

Найдем векторное произведение 2-х векторов с помощью функций MS EXCEL. Также создадим таблицу для проверки

векторов

на коллинеарность.

Сначала немного теории. Векторным произведением двух векторов

а

и

b

, заданных в прямоугольной системе координат трехмерного пространства, называется такой вектор

c

, что:

1. он

   перпендикулярен

   обоим векторам
   
   а
   
   и
   
   b
   
   ;

2. длина вектора
   
   с
   
   равна произведению длин векторов
   
   а
   
   и
   
   b
   
   на синус угла между ними;
3. вектор
   
   с
   
   направлен так, что тройка векторов
   
   а
   
   ,
   
   b
   
   и
   
   с
   
   является правой (

   с конца вектора
   
   с
   
   кратчайший поворот от вектора
   
   a
   
   к вектору
   
   b
   
   виден наблюдателю против часовой стрелки

   ).

Почему такое сложное определение? Дело в том, что результатом векторного произведения [

a

х

b

], в отличие от

скалярного

, является вектор. А для того, чтобы однозначно определить вектор нужно задать его длину (второй пункт определения) и направление (первый и третий пункты определения).

Векторное произведение

двух векторов

a

= {

a

_x

;

a

_y

;

a

_z

} и

b

= {

b

_x

;

b

_y

;

b

_z

} в декартовой системе координат можно вычислить, используя формулы:

[

a

х

b

] = {

a

_y

b

_z

—

a

_z

b

_y

;

a

_z

b

_x

—

a

_x

b

_z

;

a

_x

b

_y

—

a

_y

b

_x

}

или в матричной форме:

Теперь вычислим векторное произведение в MS EXCEL.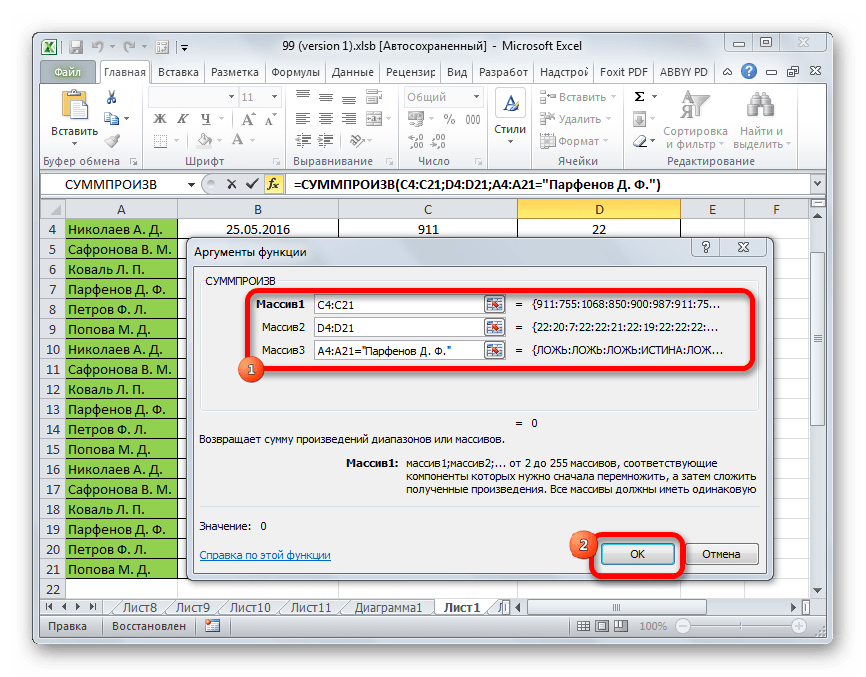 Встроенная функция к сожалению отсутствует. Кроме того, формула должна возвращать три значения, т.е. 3 координаты вектора. Это может быть реализовано только

формулой массива

(вариант, когда 3 координаты рассчитываются независимо, с использованием 3-х различных формул, очевиден, но не интересен, хотя и приведен

файле примера

).

Пусть даны координаты векторов

а

и

b

, записанные в строках 8 и 9 (см.

файл примера

).

Обратим внимание, что запись в матричной форме напоминает

вычисление обратной матрицы методом алгебраических дополнений

. Вместо единичных векторов i, j, k запишем вспомогательный вектор с координатами {1; 1; 1} и поместим его в строке 7 над векторами. Теперь у нас есть квадратная матрица А третьего порядка, для которой можно вычислить обратную матрицу.

Попробуем использовать функцию

МОБР()

для вычисления векторного произведения. Заметим, что три слагаемых из определения векторного произведения в матричной форме совпадают со значениями верхней строки матрицы алгебраических дополнений.

Примечание

: Напомним, что алгебраическое дополнение A

_ij

вычисляется по формуле A

_ij

=(-1)

^i+j

*М

_ij

(где М — соответствующий минор, т.е. определитель, состоящий из элементов матрицы А за исключением всех элементов, расположенных на строке i и в столбце j).

Так как обратная матрица вычисляется по формуле:

то имея обратную матрицу, для вычисления верхней строки матрицы алгебраических дополнений и, соответственно, координат вектора

с

, необходимо ее

транспонировать

, а затем умножить ее на определитель матрицы А (той, что содержит координаты наших векторов

а

и

b

и единичный вектор).

Это реализовано с помощью

формулы массива

=ТРАНСП(МОБР(B7:D9))*МОПРЕД(B7:D9)

Коллинеарность векторов

Если два вектора коллинеарны, т.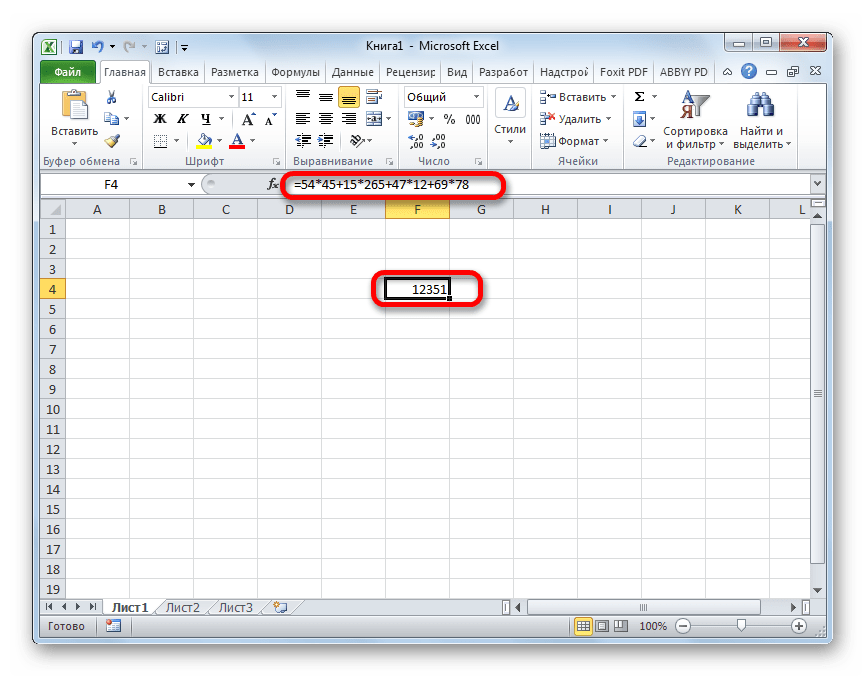 е. лежат на параллельных прямых, то их векторное произведение равно 0. В

файле примеров

приведена таблица для проверки векторов на коллинеарность.

Нахождение длины вектора с — результата векторного произведения

Из определения векторного произведения

длина вектора

с

равна произведению длин векторов

а

и

b

на синус угла между ними.

Примечание

: Как вычислить длины векторов по их координатам показано в статье

Вычисление длины (модуля) вектора в MS EXCEL

.

Синус угла найдем через тригонометрическую формулe sin

²

x+cos

²

x=1

Конечно, можно также сначала найти векторное произведение, а затем длину полученного вектора. Естественно, оба метода расчета дают одинаковые результаты.

Создать простую формулу в Excel

Excel

Формулы и функции

Формулы

Формулы

Создать простую формулу в Excel

Excel для Microsoft 365 Excel для Microsoft 365 для Mac Excel 2021 Excel 2021 для Mac Excel 2019 Excel 2019 для Mac Excel 2016 Excel 2016 для Mac Excel 2013 Excel 2010 Excel 2007 Excel для Mac 2011 Дополнительно.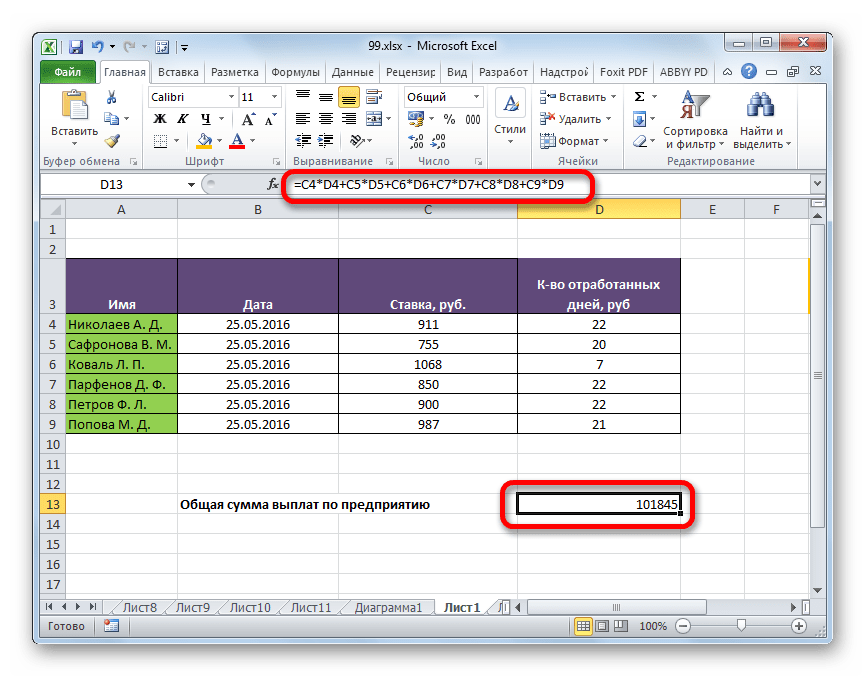 ..Меньше

Вы можете создать простую формулу для сложения, вычитания, умножения или деления значений на листе. Простые формулы всегда начинаются со знака равенства ( = ), за которым следуют константы, представляющие собой числовые значения, и операторы вычисления, такие как плюс ( + ), минус ( — ), звездочка ( * ) или косая черта. ( / ) знаки.

Возьмем пример простой формулы.

1. На рабочем листе щелкните ячейку, в которую вы хотите ввести формулу.

2. Введите = (знак равенства), а затем константы и операторы (до 8192 символов), которые вы хотите использовать в расчетах.

   В нашем примере введите =1+1 .

   Примечания:

   • Вместо того, чтобы вводить константы в формулу, вы можете выбрать ячейки, содержащие значения, которые вы хотите использовать, и ввести операторы между выбранными ячейками.

   • В соответствии со стандартным порядком математических операций умножение и деление выполняются перед сложением и вычитанием.

3. Нажмите Введите (Windows) или Верните (Mac).

Возьмем еще один вариант простой формулы. Тип =5+2*3 в другой ячейке и нажмите Введите или Верните .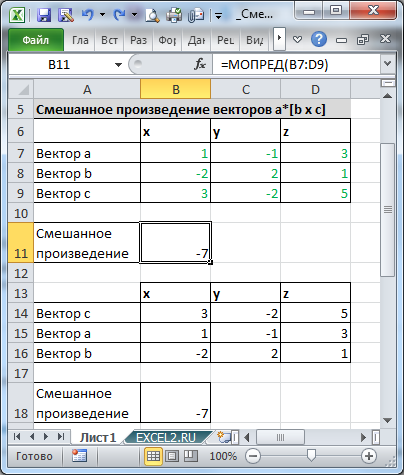 Excel умножает два последних числа и прибавляет к результату первое число.

Использовать автосумму

Вы можете использовать автосумму для быстрого суммирования столбца, строки или чисел. Выберите ячейку рядом с числами, которые вы хотите просуммировать, щелкните AutoSum на вкладке Home , нажмите Enter (Windows) или Return (Mac), и все!

Когда вы нажимаете Автосумма , Excel автоматически вводит формулу (которая использует функцию СУММ) для суммирования чисел.

Примечание. Вы также можете ввести ALT+= (Windows) или ALT++= (Mac) в ячейку, и Excel автоматически вставит функцию СУММ.

Вот пример. Чтобы добавить числа за январь в этот бюджет развлечений, выберите ячейку B7, ячейку непосредственно под столбцом чисел. Затем нажмите Автосумма . В ячейке B7 появляется формула, и Excel выделяет ячейки, которые вы суммируете.

Нажмите Enter, чтобы отобразить результат (95,94) в ячейке B7. Вы также можете увидеть формулу в строке формул в верхней части окна Excel.

Примечания:

• Чтобы просуммировать столбец чисел, выберите ячейку непосредственно под последним числом в столбце. Чтобы просуммировать ряд чисел, выберите ячейку сразу справа.

• Создав формулу, вы можете скопировать ее в другие ячейки вместо того, чтобы вводить ее снова и снова. Например, если вы скопируете формулу из ячейки B7 в ячейку C7, формула в ячейке C7 автоматически подстроится под новое место и вычислит числа в ячейках C3:C6.

• org/ListItem»>

  Вы также можете использовать автосумму для нескольких ячеек одновременно. Например, вы можете выделить как ячейку B7, так и ячейку C7, нажать AutoSum и суммировать оба столбца одновременно.

Скопируйте данные примера из следующей таблицы и вставьте их в ячейку A1 нового рабочего листа Excel. При необходимости вы можете настроить ширину столбцов, чтобы увидеть все данные.

Примечание. Чтобы формулы отображали результаты, выберите их, нажмите F2, а затем нажмите Введите (Windows) или Верните (Mac).

92

Нужна дополнительная помощь?

Вы всегда можете обратиться к эксперту в техническом сообществе Excel или получить поддержку в сообществе ответов.

Google Sheets: онлайн-редактор электронных таблиц

Посмотрите, что вы можете делать с Google Sheets

Создавайте индивидуальные решения

Ускорьте рабочие процессы, создав бизнес-приложения и средства автоматизации. Используйте AppSheet для создания пользовательских приложений поверх Таблиц без написания кода. Или добавьте пользовательские функции, пункты меню и макросы с помощью Apps Script.

Всегда работайте со свежими данными

В Таблицах все всегда работают с последней версией электронной таблицы. А благодаря тому, что изменения автоматически сохраняются в истории версий, их легко отменить или даже просмотреть историю изменений отдельной ячейки электронной таблицы.

Беспрепятственно подключайтесь к критически важным данным

Получайте и анализируйте данные из других используемых вами инструментов, например данные о клиентах из Salesforce. Корпоративные клиенты также могут использовать Connected Sheets для анализа миллиардов строк данных BigQuery в Sheets — без написания кода.

Безопасность, соответствие требованиям и конфиденциальность

Частный по дизайну

Таблицы придерживаются тех же надежных обязательств в отношении конфиденциальности и защиты данных, что и остальные корпоративные сервисы Google Cloud.

Вы контролируете свои данные.

Мы никогда не используем содержимое ваших Таблиц в рекламных целях.

Мы никогда не передаем вашу персональную информацию третьим лицам.

Найдите план, который подходит именно вам

Google Таблицы являются частью Google Workspace

Сотрудничайте из любого места, на любом устройстве

Получайте доступ, создавайте и редактируйте свои электронные таблицы, где бы вы ни находились — с любого мобильного устройства, планшета или компьютера — даже в автономном режиме.