Формула xl: Все формулы эксель
Содержание
Формула 185/65/15 H 92 Energy XL
Описание
Автомобильная шина Formula Energy предназначена для использования на скоростных легковых автомобилях малого и среднего класса в течение летнего периода. Новинка от производителя шин с мировым именем Pirelli вызвала небывалый интерес среди потенциальных покупателей не только из-за брендового названия, но в большей степени благодаря уникальности технических характеристик.
Немалый опыт работы на спортивном поприще позволил конструкторам компании Pirelli разработать модель шины, идеально сочетающую высокие скоростные характеристики, безопасность управления, а также экологическую чистоту продукции. Немаловажное значение играет также оптимальное соотношение качества и стоимости изделия, что делает шины Formula Energy доступными для широкого круга потребителей.
Оригинальный дизайн рисунка протектора Formula Energy в сочетании с применением перспективных конструкционных материалов гарантируют продолжительный срок службы шины, отличную управляемость на дорогах с твердым покрытием независимо от степени влажности, сокращение длины тормозного пути в случае экстренной остановки. Кроме выдающихся скоростных и динамических характеристик, протектор выглядит очень стильно, подчеркивая элегантность автомобилей спортивного класса.
Кроме выдающихся скоростных и динамических характеристик, протектор выглядит очень стильно, подчеркивая элегантность автомобилей спортивного класса.
Снижение сопротивления качению более чем на 20% дает реальную экономию топлива, поэтому уменьшаются вредные выбросы в атмосферу.
Разработчикам удалось снизить внутренний шум до 1 дБ – это явный плюс в отношении оценки комфортабельности. По сравнению с шинами аналогичного класса от других производителей, Formula Energy имеет меньший вес (примерно на 10%).
Модельный ряд шин Formula Energy представлен в нескольких типоразмерах, отличающихся радиусом, шириной рабочей поверхности, а также индексом скорости. К слову о скорости: индекс скорости для шин Pirelli Energy Formula находится в диапазоне от 190-300 км/час (от T до Y), что явно указывает на спортивную ориентацию модели.
ОСНОВНЫЕ ОСОБЕННОСТИ FORMULA ENERGY
– Летняя модель для спортивных автомобилей малого и среднего класса;
– Хорошие скоростные и динамические характеристики на дорогах с твердым покрытием;
– Высокая безопасность, маневренность и точность управления автомобиля;
– Низкий коэффициент внутреннего шума;
– Экономия топлива и снижение вредных выбросов в атмосферу;
– Экологическая чистота;
– Продолжительный срок эксплуатации.
* Внимание: летние шины не российского происхождения могут быть промаркированы обозначением M+S
Спецификация шины
Основное
SKU: 86017045023
Бренд: FORMULA
Модель: Energy
Сезон: Летние
Индекс нагрузки: 92 — 630 кг | x4 — 2520 кг
Индекс скорости: —
Назначение
Технологии
XL / Усиленные боковины:
Да
Технология ранфлет:
Нет
Коммерческие / Усиленные
Нет
Доставка
| Вид доставки | Стоимость | Срок поставки |
| Курьер. Доставка до подъезда (Ростов-на-Дону) | бесплатно | 1-2 дня |
| Курьер. Доставка до подъезда (Батайск) | бесплатно | 1-2 дня |
| Самовывоз (Батайск, Энгельса, 353) | бесплатно | 0 дней |
Гарантия
Стандартная гарантия
Гарантийный срок — это срок, во время которого покупатель, обнаружив недостаток товара, имеет право потребовать от продавца или изготовителя принять меры по устранению дефекта. Продавец должен устранить недостатки, если не будет доказано, что они возникли вследствие нарушений покупателем правил эксплуатации.
Продавец должен устранить недостатки, если не будет доказано, что они возникли вследствие нарушений покупателем правил эксплуатации.
Кто устанавливает гарантийный срок
Гарантийный срок устанавливается на каждый товар производителем и указывается в документах или гарантийных документах, выдаваемых продавцом.
Зимняя резина Formula R17 в Санкт-Петербурге
Formula Winter 225/45 R17 94H XL
Нешипованные
Новая модель
3 шт. в наличии
Цена:
7.422 ₽
Formula Ice 225/50 R17 98T XL
Шипованные
Видео
60 шт. в наличии
Цена:
8.647 ₽
Комплект:
34.588 ₽
Formula Ice 215/50 R17 95T XL
Шипованные
Видео
40 шт. в наличии
в наличии
Цена:
8.755 ₽
Комплект:
35.020 ₽
Formula Ice 225/65 R17 102T
Шипованные
Видео
50 шт. в наличии
Цена:
9.056 ₽
Комплект:
36.224 ₽
Formula Ice 225/55 R17 101T XL
Шипованные
Видео
60 шт. в наличии
Цена:
9.295 ₽
Комплект:
37.180 ₽
Formula Ice 215/55 R17 98T XL
Шипованные
Видео
48 шт. в наличии
Цена:
9.413 ₽
Комплект:
37.652 ₽
Formula Ice 225/60 R17 99T
Шипованные
Видео
44 шт. в наличии
в наличии
Цена:
9.508 ₽
Комплект:
38.032 ₽
Formula Ice 235/65 R17 108T XL
Шипованные
Видео
20 шт. в наличии
Цена:
9.700 ₽
Комплект:
38.800 ₽
Formula Ice 215/60 R17 100T XL
Шипованные
Видео
50 шт. в наличии
Цена:
9.727 ₽
Комплект:
38.908 ₽
Formula Ice 235/55 R17 103T XL
Шипованные
Видео
50 шт. в наличии
Цена:
10.171 ₽
Комплект:
40.684 ₽
Formula Ice 265/65 R17 112T
Шипованные
Видео
32 шт. в наличии
в наличии
Цена:
11.498 ₽
Комплект:
45.992 ₽
По размерам: Зимние шины Formula R14 | Зимние шины Formula R15 | Зимние шины Formula R16 | Зимние шины Formula R18
Другие сезоны: Летние шины Formula R17
Популярное: зимняя резина R16 и другие размеры
По типу: Нешипованная зимняя резина (липучка)
Формула индуктивного реактивного сопротивления и расчеты
Любая катушка индуктивности сопротивляется изменениям переменного тока, и это приводит к тому, что она создает для него импеданс.
Учебное пособие по индуктивности и трансформатору Включает:
Индуктивность
Символы
закон Ленца
Собственная индуктивность
Расчет индуктивного сопротивления
Теория индуктивного сопротивления
Индуктивность провода и катушки
Взаимная индуктивность
Трансформеры
Катушка индуктивности сопротивляется потоку переменного тока за счет своей индуктивности. Любая катушка индуктивности сопротивляется изменению тока в результате закона Ленца.
Любая катушка индуктивности сопротивляется изменению тока в результате закона Ленца.
Степень, в которой индуктор препятствует протеканию тока, обусловлена его индуктивным реактивным сопротивлением.
Индуктивное реактивное сопротивление зависит от частоты и возрастает с увеличением частоты, но его можно легко рассчитать с помощью простых формул.
Индуктивное реактивное сопротивление
Эффект, благодаря которому протекание переменного или изменяющегося тока в катушке индуктивности уменьшается, называется ее индуктивным реактивным сопротивлением. Любому изменению тока в катушке индуктивности будет препятствовать связанная с ней индуктивность.
Причину этого индуктивного сопротивления можно легко увидеть, исследуя собственную индуктивность и ее влияние в цепи.
Когда на катушку индуктивности подается переменный ток, собственная индуктивность вызывает индуцированное напряжение. Это напряжение пропорционально индуктивности, и в соответствии с законом Ленца индуцированное напряжение противоположно приложенному напряжению.
Таким образом, индуцированное напряжение будет работать против напряжения, вызывающего протекание тока, и, таким образом, оно будет препятствовать протеканию тока, и говорят, что индуктор имеет определенное индуктивное реактивное сопротивление.
Формулы индуктивного сопротивления
Хотя идеальных катушек индуктивности не существует, полезно представить себе одну, чтобы взглянуть на формулы и расчеты, связанные с катушками индуктивности и индуктивностью. В этом случае идеальная катушка индуктивности имеет только индуктивность, но не имеет сопротивления или емкости.
Индуктивное сопротивление катушки индуктивности зависит от ее индуктивности, а также от применяемой частоты. Реактивное сопротивление увеличивается линейно с частотой. Другими словами, удвоение частоты приведет к удвоению индуктивного сопротивления конкретной катушки, провода и т. д.
Именно по этой причине на очень высоких частотах индуктивное реактивное сопротивление для длин проводов становится важным, и в некоторых цепях необходимо обеспечить, чтобы соединения были как можно ближе друг к другу.
Это можно выразить в виде формулы для расчета реактивного сопротивления на определенной частоте.
XL=2πfL
Где:
XL = индуктивное сопротивление в омах, Ом
π = греческая буква Пи, 3,142
f = частота в Гц
L = индуктивность в генри
Подробнее о . . . . теория индуктивного сопротивления.
Закон Ома и индуктивное сопротивление
Если на эту идеальную катушку индуктивности подается изменяющийся сигнал, такой как синусоида, реактивное сопротивление препятствует протеканию тока и подчиняется закону Ома.
Если единственным присутствующим компонентом является катушка индуктивности, то достаточно просто применить закон Ома и рассчитать напряжение или ток и т. д., зная две другие переменные. Также возможно рассчитать реактивное сопротивление, зная напряжение и ток.
Где:
X L = индуктивное сопротивление в омах, Ом
V = напряжение в вольтах
I = ток в амперах
Можно использовать треугольник закона Ома. Это простой способ запоминания уравнения закона Ома. Просто возьмите переменную, которую необходимо вычислить, и
Это простой способ запоминания уравнения закона Ома. Просто возьмите переменную, которую необходимо вычислить, и
Треугольник используется для сокрытия или выделения необходимой переменной. Затем можно увидеть оставшиеся два. Если две переменные находятся рядом друг с другом, они перемножаются.
Если переменные расположены одна над другой, то верхняя делится на нижнюю. Это можно резюмировать на общей сводной диаграмме того, как треугольник закона Ома может быть использован для индуктивного реактивного сопротивления ниже.
Использование треугольника закона Ома таким образом позволяет использовать правильные расчеты и версии формул для индуктивного реактивного сопротивления при выполнении расчета в стиле закона Ома.
Добавление индуктивного сопротивления и сопротивления
Реальная катушка индуктивности будет иметь некоторое сопротивление, или катушки индуктивности могут быть объединены с резисторами для создания комбинированной сети. В любом из этих случаев необходимо знать полное сопротивление цепи.
Поскольку ток и напряжение в катушке индуктивности не совпадают по фазе на 90° (ток отстает от напряжения), индуктивное реактивное сопротивление и сопротивление не могут быть добавлены напрямую.
Сложение индуктивного реактивного сопротивления и сопротивления постоянному току
Сложение индуктивного реактивного сопротивления и сопротивления постоянного тока осуществляется векторно
Из диаграммы видно, что эти две величины необходимо сложить вместе векторно. Это означает, что индуктивное сопротивление и сопротивление необходимо возвести в квадрат, добавить и затем извлечь квадратный корень из полученного результата:
VTotal2=VL2+VR2
Это можно переписать в более удобный формат:
VTotal=VL2+VR2
Результирующая комбинация сопротивления и индуктивного сопротивления называется импедансом и снова измеряется в омах.
При использовании и проектировании цепей, содержащих катушки индуктивности, часто необходимо посмотреть на индуктивное сопротивление, рассчитать его по приведенным выше формулам, а затем добавить его к чистому сопротивлению, чтобы получить общий импеданс.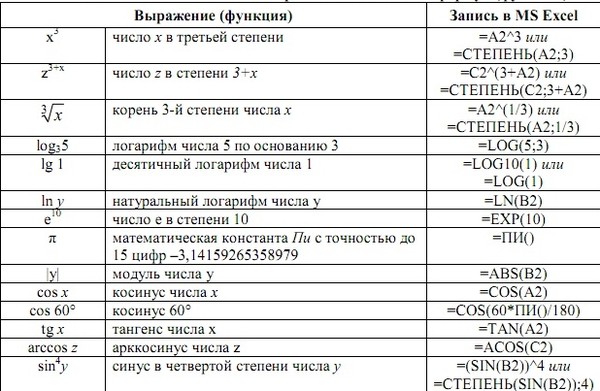 Как таковые, эти формулы особенно полезны.
Как таковые, эти формулы особенно полезны.
Дополнительные основные понятия и руководства по электронике:
Напряжение
Текущий
Сила
Сопротивление
Емкость
Индуктивность
Трансформеры
Децибел, дБ
Законы Кирхгофа
Q, добротность
РЧ-шум
Сигналы
Вернуться в меню основных понятий электроники . . .
Формулы Excel: сложные формулы
Урок 3: сложные формулы
/en/excelformulas/simple-formulas/content/
Введение
Простая формула — это математическое выражение с одним оператором, например 7+9 . Сложная формула содержит более одного математического оператора, например 5+2*8 . Когда в формуле есть более одной операции, порядок операций сообщает электронной таблице, какую операцию следует вычислить первой. Чтобы использовать сложные формулы, вам нужно будет понять порядок операций.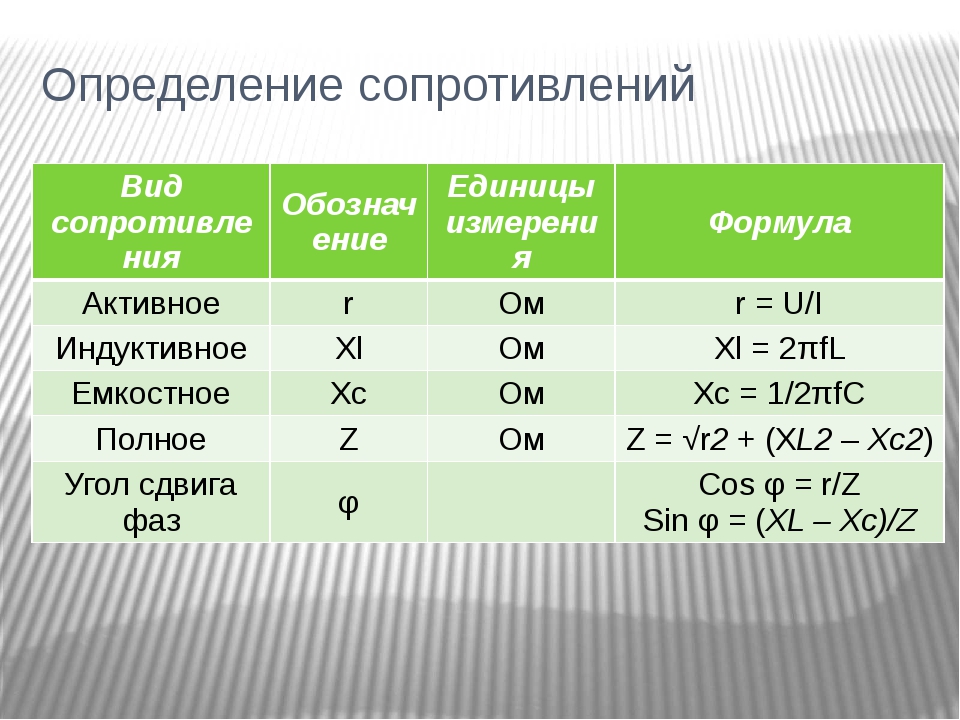
Необязательно: загрузите файл примера для этого урока. 92, например)
05050505050105.
PEMDAS или P аренда E извините M y D ухо A unt S союзник.
Щелкните стрелки в слайд-шоу ниже, чтобы узнать больше о том, как порядок операций используется для вычисления сложных формул. 92=4.
Далее мы решим любое умножение и деление слева направо. Поскольку операция деления предшествует умножению, она вычисляется первой: 3/4=0,75.
Теперь мы вычислим оставшуюся операцию умножения: 0,75*4=3.
Далее мы вычислим любое сложение или вычитание, снова работая слева направо. Сначала идет сложение: 10+3=13.
Наконец, у нас осталась одна операция вычитания: 13-1=12.
А теперь у нас есть ответ: 12. Это точно такой же результат, который вы получили бы, если бы ввели формулу в электронную таблицу.
Теперь давайте рассмотрим пару примеров, которые показывают, как порядок операций может повлиять на результат.
Использование скобок в формуле может быть очень важным. Из-за порядка операций он может полностью изменить ответ. Давайте попробуем решить ту же задачу, что и выше, но на этот раз мы добавим круглые скобки в последнюю часть.
Создание сложных формул
В приведенном ниже примере мы продемонстрируем сложную формулу, используя порядок операций. Здесь мы хотим рассчитать стоимость налога с продаж для счета за питание. Для этого мы напишем нашу формулу как =(D2+D3)*0,075 в ячейке D4 . Эта формула суммирует цены наших товаров, а затем умножает это значение на налоговую ставку 7,5% (которая записывается как 0,075) для расчета стоимости налога с продаж.
Эта формула суммирует цены наших товаров, а затем умножает это значение на налоговую ставку 7,5% (которая записывается как 0,075) для расчета стоимости налога с продаж.
Электронная таблица следует порядку операций и сначала добавляет значения в круглых скобках: (44,85+39,90) = 84,75 долл. США . Затем это значение умножается на налоговую ставку: $84,75*0,075 . Результат покажет, что налог с продаж составляет $6,36 .
Особенно важно вводить сложные формулы с правильным порядком операций. В противном случае электронная таблица не будет точно рассчитывать результаты. В нашем примере, если круглых скобок не включены, сначала вычисляется умножение, и результат неверен. Круглые скобки — лучший способ определить, какие вычисления будут выполняться в формуле первыми.
Чтобы создать сложную формулу, используя порядок операций:
В приведенном ниже примере мы будем использовать ссылок на ячейки вместе с числовыми значениями , чтобы создать сложную формулу, которая будет вычислять общую стоимость счета за питание. . Формула рассчитает стоимость каждого пункта меню и сложит эти значения.
. Формула рассчитает стоимость каждого пункта меню и сложит эти значения.
- Выберите ячейку , которая будет содержать формулу. В нашем примере мы выберем ячейку C4 9.0113 .
- Введите формулу . В нашем примере мы введем =B2*C2+B3*C3 . Эта формула будет следовать порядку операций, сначала выполняя умножение: 2,29*20 = 45,80 и 3,49*35 = 122,15 . Затем он сложит эти значения вместе, чтобы вычислить общее количество: 45,80+122,15 .
- Дважды проверьте формулу на точность, затем нажмите Введите на клавиатуре. Формула вычислит и отобразит результат . В нашем примере результат показывает, что общая стоимость заказа составляет 167,95 $ .
Вы можете добавить круглых скобок к любому уравнению, чтобы его было легче читать.

