Как решать формулы в excel: Обзор формул — Служба поддержки Майкрософт
Содержание
Решение системы уравнений в Excel
4133
16.10.2022
Скачать пример
Возможно вы слышали о нобелевском лауреате, психологе и исследователе по имени Дэниель Канеман. Канеман занимался наукой, которую называют термином «поведенческая экономика», т.е. изучал реакции, поведение и суждения людей в типовых жизненных (и экономических) ситуациях и условиях неопределенности.
В его книге, которая называется «Думай медленно — решай быстро» (очень рекомендую, кстати) в качестве одного из примеров когнитивных искажений — несознательной автоматической реакции — приводится следующая задача:
Бейсбольная бита и мяч стоят вместе 1 доллар 10 центов.
Бита дороже мяча на 1 доллар.
Сколько стоит мяч?
Подозреваю, что вашей первой рефлекторной мыслью, скорее всего, будет «10 центов!» 🙂 Но весьма скоро, я уверен, вы сообразите, что на самом деле всё не так примитивно и для получения ответа нужно решить простую систему уравнений (здесь b — это бита, а m — это мяч):
Конечно можно «тряхнуть стариной» и решить всё вручную на бумажке через подстановку переменных — как-то так:
Но, во-первых, на практике уравнения могут быть сложнее и переменных может оказаться сильно больше двух и, во-вторых, у нас с вами есть Microsoft Excel — универсальный мега-инструмент, величайшее изобретение человечества. Так что давайте-ка лучше разберём как решить нашу задачу с его помощью.
Способ 1. Матричные функции МУМНОЖ и МОБР
Само собой, изобретать велосипед тут не надо — прогрессивное человечество в лице математиков давным-давно придумало кучу способов для решения подобных задач. В частности, если уравнения в нашей системе линейные (т.е. не используют степени, логарифмы, тригонометрические функции типа sin, cos и т.д.), то можно использовать метод Крамера.
В частности, если уравнения в нашей системе линейные (т.е. не используют степени, логарифмы, тригонометрические функции типа sin, cos и т.д.), то можно использовать метод Крамера.
Сначала записываем числовые коэффициенты, стоящие перед нашими переменными в виде матрицы (в нашем случае — размером 2х2, в общем случае — может быть и больше).
Затем находим для неё так называемую обратную матрицу , т.е. матрицу, при умножении которой на исходную матрицу коэффициентов получается единица. В Excel это легко сделать с помощью стандартной математической функции МОБР (MINVERSE):
Здесь важно отметить, что если у вас свежая версия Excel 2021 или Excel 365, то достаточно ввести эту функцию обычным образом в первую ячейку (G7) — сразу получится динамический массив с обратной матрицей 2х2. Если же у вас более старая версия Excel, то эту функцию нужно обязательно вводить как формулу массива, а именно:
- Выделить диапазон для результатов — G7:H8
- Ввести функцию =МОБР(B7:C8) в строку формул
- Нажать на клавиатуре сочетание клавиш Ctrl+Shift+Enter
Замечательное свойство обратной матрицы состоит в том, что если умножить её на значения правых частей наших уравнений (свободные члены), то мы получим значения переменных, при которых левые и правые части уравнений будут равны, т. е. решения нашей задачи. Выполнить такое матричное умножение можно с помощью ещё одной стандартной экселевской функции МУМНОЖ (MMULT):
е. решения нашей задачи. Выполнить такое матричное умножение можно с помощью ещё одной стандартной экселевской функции МУМНОЖ (MMULT):
Если у вас старая версия Excel, то не забудьте также ввести её в режиме формулы массива, т.е. сначала выделить диапазон K7:K8, а после ввода функции нажать сочетание клавиш Ctrl+Shift+Enter.
Само собой, уравнений и переменных может быть больше, да и посчитать всё можно сразу в одной формуле, вложив используемые функции одна в другую:
Не так уж и сложно, правда? Однако надо понимать, что этот метод подходит только для решения систем линейных уравнений. Если у вас в уравнениях используются функции посложнее четырех базовых математических действий, то зачастую проще будет пойти другим путем — через подбор.
Способ 2. Подбор надстройкой «Поиск решения» (Solver)
Принципиально другой способ решения подобных задач — это итерационные методы, т. е. последовательный подбор значений переменных, чтобы после подстановки их в наши уравнения мы получили верные равенства. Само собой, подбор имеется ввиду не тупой и долгий (брутфорс), а умный и быстрый, благо математики, опять же, давным-давно придумали кучу различных методов для решения таких задач буквально за несколько итераций.
е. последовательный подбор значений переменных, чтобы после подстановки их в наши уравнения мы получили верные равенства. Само собой, подбор имеется ввиду не тупой и долгий (брутфорс), а умный и быстрый, благо математики, опять же, давным-давно придумали кучу различных методов для решения таких задач буквально за несколько итераций.
В Microsoft Excel некоторые из этих методов реализованы в стандартной надстройке Поиск решения (Solver). Её можно подключить через Файл — Параметры — Надстройки — Перейти (File — Options — Add-ins — Go to) или на вкладке Разработчик — Надстройки (Developer — Add-ins).
Давайте рассмотрим её использование на следующей задаче. Предположим, что нам с вами нужно решить вот такую систему из двух нелинейных уравнений:
Подготавливаем основу для оптимизации в Excel:
Здесь:
- В жёлтых ячейках C9:C10 лежат текущие значения наших переменных, которые и будут подбираться в процессе оптимизации.
 В качестве стартовых можно взять любые значения, например, нули или единицы — роли не играет. Для удобства, кстати, этим ячейкам можно дать имена, назвав их именами переменных x и y, — для этого выделите диапазон C9:C10 и выберите команду Формулы — Создать из выделенного — Слева (Formulas — Create from selection — Left column).
В качестве стартовых можно взять любые значения, например, нули или единицы — роли не играет. Для удобства, кстати, этим ячейкам можно дать имена, назвав их именами переменных x и y, — для этого выделите диапазон C9:C10 и выберите команду Формулы — Создать из выделенного — Слева (Formulas — Create from selection — Left column). - В зелёных ячейках E9:E10 введены наши уравнения с использованием либо прямых ссылок на жёлтые ячейки переменных, либо созданных имён (так нагляднее). В результате мы видим, чему равны наши уравнения при текущих значениях переменных.
- В синих ячейках F9:F10 введены значения правых частей наших уравнений, к которым мы должны стремиться.
Теперь запускаем нашу надстройку на вкладке Данные — Поиск решения (Data — Solver) и вводим в появившемся диалоговом окне следующие параметры:
- Оптимизировать целевую функцию (Set target cell) — любая из двух наших зелёных ячеек с уравнениями, например E9.

- Изменяя ячейки переменных (By changing cells) — жёлтые ячейки с текущими значениями переменных, которыми мы «играем».
- Добавляем ограничение с помощью кнопки Добавить (Add) и задаём равенство левой и правой части наших уравнений, т.е. зелёного и голубого диапазонов.
- В качестве метода решения выбираем Поиск решения нелинейных задач методом ОПГ, т.к. уравнения у нас нелинейные. Для линейных можно смело выбирать симплекс-метод.
После нажатия на кнопку Найти решение (Solve) через пару мгновений (или не пару — это зависит от сложности задачи) мы должны увидеть окно с результатами. Если решение найдено, то в жёлтых ячейках отобразятся подобранные значения наших переменных:
Обратите внимание, что поскольку мы здесь используем итерационные, а не аналитические методы, то зеленые ячейки не совсем равны голубым, т.е. найденное решение не абсолютно точно. На практике, конечно же, такой точности вполне достаточно для большинства задач, и если необходимо, её можно настроить, вернувшись в окно Поиск решения и нажав кнопку Параметры (Options).
Как сделать уравнение в excel?
Содержание
- 1 Варианты решений
- 1.1 Способ 1: матричный метод
- 1.2 Способ 2: подбор параметров
- 1.3 Способ 3: метод Крамера
- 1.4 Способ 4: метод Гаусса
- 1.5 Помогла ли вам эта статья?
- 2 Решение уравнений методом подбора параметров Excel
- 3 Как решить систему уравнений матричным методом в Excel
- 4 Решение системы уравнений методом Крамера в Excel
- 5 Решение систем уравнений методом Гаусса в Excel
- 6 Примеры решения уравнений методом итераций в Excel
Умение решать системы уравнений часто может принести пользу не только в учебе, но и на практике. В то же время, далеко не каждый пользователь ПК знает, что в Экселе существует собственные варианты решений линейных уравнений. Давайте узнаем, как с применением инструментария этого табличного процессора выполнить данную задачу различными способами.
Варианты решений
Любое уравнение может считаться решенным только тогда, когда будут отысканы его корни. В программе Excel существует несколько вариантов поиска корней. Давайте рассмотрим каждый из них.
В программе Excel существует несколько вариантов поиска корней. Давайте рассмотрим каждый из них.
Способ 1: матричный метод
Самый распространенный способ решения системы линейных уравнений инструментами Excel – это применение матричного метода. Он заключается в построении матрицы из коэффициентов выражений, а затем в создании обратной матрицы. Попробуем использовать данный метод для решения следующей системы уравнений:
14x1+2x2+8x4=218
7x1-3x2+5x3+12x4=213
5x1+x2-2x3+4x4=83
6x1+2x2+x3-3x4=21
- Заполняем матрицу числами, которые являются коэффициентами уравнения. Данные числа должны располагаться последовательно по порядку с учетом расположения каждого корня, которому они соответствуют. Если в каком-то выражении один из корней отсутствует, то в этом случае коэффициент считается равным нулю. Если коэффициент не обозначен в уравнении, но соответствующий корень имеется, то считается, что коэффициент равен 1. Обозначаем полученную таблицу, как вектор A.

- Отдельно записываем значения после знака «равно». Обозначаем их общим наименованием, как вектор B.
- Теперь для нахождения корней уравнения, прежде всего, нам нужно отыскать матрицу, обратную существующей. К счастью, в Эксель имеется специальный оператор, который предназначен для решения данной задачи. Называется он МОБР. Он имеет довольно простой синтаксис:
=МОБР(массив)Аргумент «Массив» — это, собственно, адрес исходной таблицы.
Итак, выделяем на листе область пустых ячеек, которая по размеру равна диапазону исходной матрицы. Щелкаем по кнопке «Вставить функцию», расположенную около строки формул.
- Выполняется запуск Мастера функций. Переходим в категорию «Математические». В представившемся списке ищем наименование «МОБР». После того, как оно отыскано, выделяем его и жмем на кнопку «OK».
- Запускается окно аргументов функции МОБР. Оно по числу аргументов имеет всего одно поле – «Массив». Тут нужно указать адрес нашей таблицы.
 Для этих целей устанавливаем курсор в это поле. Затем зажимаем левую кнопку мыши и выделяем область на листе, в которой находится матрица. Как видим, данные о координатах размещения автоматически заносятся в поле окна. После того, как эта задача выполнена, наиболее очевидным было бы нажать на кнопку «OK», но не стоит торопиться. Дело в том, что нажатие на эту кнопку является равнозначным применению команды Enter. Но при работе с массивами после завершения ввода формулы следует не кликать по кнопке Enter, а произвести набор сочетания клавиш Ctrl+Shift+Enter. Выполняем эту операцию.
Для этих целей устанавливаем курсор в это поле. Затем зажимаем левую кнопку мыши и выделяем область на листе, в которой находится матрица. Как видим, данные о координатах размещения автоматически заносятся в поле окна. После того, как эта задача выполнена, наиболее очевидным было бы нажать на кнопку «OK», но не стоит торопиться. Дело в том, что нажатие на эту кнопку является равнозначным применению команды Enter. Но при работе с массивами после завершения ввода формулы следует не кликать по кнопке Enter, а произвести набор сочетания клавиш Ctrl+Shift+Enter. Выполняем эту операцию. - Итак, после этого программа производит вычисления и на выходе в предварительно выделенной области мы имеем матрицу, обратную данной.
- Теперь нам нужно будет умножить обратную матрицу на матрицу B, которая состоит из одного столбца значений, расположенных после знака «равно» в выражениях. Для умножения таблиц в Экселе также имеется отдельная функция, которая называется МУМНОЖ. Данный оператор имеет следующий синтаксис:
=МУМНОЖ(Массив1;Массив2)Выделяем диапазон, в нашем случае состоящий из четырех ячеек.
 Далее опять запускаем Мастер функций, нажав значок «Вставить функцию».
Далее опять запускаем Мастер функций, нажав значок «Вставить функцию». - В категории «Математические», запустившегося Мастера функций, выделяем наименование «МУМНОЖ» и жмем на кнопку «OK».
- Активируется окно аргументов функции МУМНОЖ. В поле «Массив1» заносим координаты нашей обратной матрицы. Для этого, как и в прошлый раз, устанавливаем курсор в поле и с зажатой левой кнопкой мыши выделяем курсором соответствующую таблицу. Аналогичное действие проводим для внесения координат в поле «Массив2», только на этот раз выделяем значения колонки B. После того, как вышеуказанные действия проведены, опять не спешим жать на кнопку «OK» или клавишу Enter, а набираем комбинацию клавиш Ctrl+Shift+Enter.
- После данного действия в предварительно выделенной ячейке отобразятся корни уравнения: X1, X2, X3 и X4. Они будут расположены последовательно. Таким образом, можно сказать, что мы решили данную систему. Для того, чтобы проверить правильность решения достаточно подставить в исходную систему выражений данные ответы вместо соответствующих корней.
 2+4*x-132
2+4*x-132 Вместо значения «X» подставляем адрес той ячейки, где расположено число 0, принятое нами за x.
- Переходим во вкладку «Данные». Жмем на кнопку «Анализ «что если»». Эта кнопка размещена на ленте в блоке инструментов «Работа с данными». Открывается выпадающий список. Выбираем в нем позицию «Подбор параметра…».
- Запускается окно подбора параметров. Как видим, оно состоит из трех полей. В поле «Установить в ячейке» указываем адрес ячейки, в которой находится формула f(x), рассчитанная нами чуть ранее. В поле «Значение» вводим число «0». В поле «Изменяя значения» указываем адрес ячейки, в которой расположено значение x, ранее принятое нами за 0. После выполнения данных действий жмем на кнопку «OK».
- После этого Эксель произведет вычисление с помощью подбора параметра. Об этом сообщит появившееся информационное окно. В нем следует нажать на кнопку «OK».
- Результат вычисления корня уравнения будет находиться в той ячейке, которую мы назначили в поле «Изменяя значения».
 В нашем случае, как видим, x будет равен 6.
В нашем случае, как видим, x будет равен 6.
Этот результат также можно проверить, подставив данное значение в решаемое выражение вместо значения x.
Урок: Подбор параметра в Excel
Способ 3: метод Крамера
Теперь попробуем решить систему уравнений методом Крамера. Для примера возьмем все ту же систему, которую использовали в Способе 1:
14x1+2x2+8x4=218
7x1-3x2+5x3+12x4=213
5x1+x2-2x3+4x4=83
6x1+2x2+x3-3x4=21
- Как и в первом способе, составляем матрицу A из коэффициентов уравнений и таблицу B из значений, которые стоят после знака «равно».
- Далее делаем ещё четыре таблицы. Каждая из них является копией матрицы A, только у этих копий поочередно один столбец заменен на таблицу B. У первой таблицы – это первый столбец, у второй таблицы – второй и т.д.
- Теперь нам нужно высчитать определители для всех этих таблиц. Система уравнений будет иметь решения только в том случае, если все определители будут иметь значение, отличное от нуля.
 Для расчета этого значения в Экселе опять имеется отдельная функция – МОПРЕД. Синтаксис данного оператора следующий:
Для расчета этого значения в Экселе опять имеется отдельная функция – МОПРЕД. Синтаксис данного оператора следующий:=МОПРЕД(массив)Таким образом, как и у функции МОБР, единственным аргументом выступает ссылка на обрабатываемую таблицу.
Итак, выделяем ячейку, в которой будет выводиться определитель первой матрицы. Затем жмем на знакомую по предыдущим способам кнопку «Вставить функцию».
- Активируется окно Мастера функций. Переходим в категорию «Математические» и среди списка операторов выделяем там наименование «МОПРЕД». После этого жмем на кнопку «OK».
- Запускается окно аргументов функции МОПРЕД. Как видим, оно имеет только одно поле – «Массив». В это поле вписываем адрес первой преобразованной матрицы. Для этого устанавливаем курсор в поле, а затем выделяем матричный диапазон. После этого жмем на кнопку «OK». Данная функция выводит результат в одну ячейку, а не массивом, поэтому для получения расчета не нужно прибегать к нажатию комбинации клавиш Ctrl+Shift+Enter.

- Функция производит подсчет результата и выводит его в заранее выделенную ячейку. Как видим, в нашем случае определитель равен -740, то есть, не является равным нулю, что нам подходит.
- Аналогичным образом производим подсчет определителей для остальных трех таблиц.
- На завершающем этапе производим подсчет определителя первичной матрицы. Процедура происходит все по тому же алгоритму. Как видим, определитель первичной таблицы тоже отличный от нуля, а значит, матрица считается невырожденной, то есть, система уравнений имеет решения.
- Теперь пора найти корни уравнения. Корень уравнения будет равен отношению определителя соответствующей преобразованной матрицы на определитель первичной таблицы. Таким образом, разделив поочередно все четыре определителя преобразованных матриц на число -148, которое является определителем первоначальной таблицы, мы получим четыре корня. Как видим, они равны значениям 5, 14, 8 и 15. Таким образом, они в точности совпадают с корнями, которые мы нашли, используя обратную матрицу в способе 1, что подтверждает правильность решения системы уравнений.

Способ 4: метод Гаусса
Решить систему уравнений можно также, применив метод Гаусса. Для примера возьмем более простую систему уравнений из трех неизвестных:
14x1+2x2+8x3=110
7x1-3x2+5x3=32
5x1+x2-2x3=17
- Опять последовательно записываем коэффициенты в таблицу A, а свободные члены, расположенные после знака «равно» — в таблицу B. Но на этот раз сблизим обе таблицы, так как это понадобится нам для работы в дальнейшем. Важным условием является то, чтобы в первой ячейке матрицы A значение было отличным от нуля. В обратном случае следует переставить строки местами.
- Копируем первую строку двух соединенных матриц в строчку ниже (для наглядности можно пропустить одну строку). В первую ячейку, которая расположена в строке ещё ниже предыдущей, вводим следующую формулу:
=B8:E8-$B$7:$E$7*(B8/$B$7)Если вы расположили матрицы по-другому, то и адреса ячеек формулы у вас будут иметь другое значение, но вы сможете высчитать их, сопоставив с теми формулами и изображениями, которые приводятся здесь.

После того, как формула введена, выделите весь ряд ячеек и нажмите комбинацию клавиш Ctrl+Shift+Enter. К ряду будет применена формула массива и он будет заполнен значениями. Таким образом мы произвели вычитание из второй строки первой, умноженной на отношение первых коэффициентов двух первых выражений системы.
- После этого копируем полученную строку и вставляем её в строчку ниже.
- Выделяем две первые строки после пропущенной строчки. Жмем на кнопку «Копировать», которая расположена на ленте во вкладке «Главная».
- Пропускаем строку после последней записи на листе. Выделяем первую ячейку в следующей строке. Кликаем правой кнопкой мыши. В открывшемся контекстном меню наводим курсор на пункт «Специальная вставка». В запустившемся дополнительном списке выбираем позицию «Значения».
- В следующую строку вводим формулу массива. В ней производится вычитание из третьей строки предыдущей группы данных второй строки, умноженной на отношение второго коэффициента третьей и второй строки.
 В нашем случае формула будет иметь следующий вид:
В нашем случае формула будет иметь следующий вид:=B13:E13-$B$12:$E$12*(C13/$C$12)После ввода формулы выделяем весь ряд и применяем сочетание клавиш Ctrl+Shift+Enter.
- Теперь следует выполнить обратную прогонку по методу Гаусса. Пропускаем три строки от последней записи. В четвертой строке вводим формулу массива:
=B17:E17/D17Таким образом, мы делим последнюю рассчитанную нами строку на её же третий коэффициент. После того, как набрали формулу, выделяем всю строчку и жмем сочетание клавиш Ctrl+Shift+Enter.
- Поднимаемся на строку вверх и вводим в неё следующую формулу массива:
=(B16:E16-B21:E21*D16)/C16Жмем привычное уже нам сочетание клавиш для применения формулы массива.
- Поднимаемся ещё на одну строку выше. В неё вводим формулу массива следующего вида:
=(B15:E15-B20:E20*C15-B21:E21*D15)/B15Опять выделяем всю строку и применяем сочетание клавиш Ctrl+Shift+Enter.

- Теперь смотрим на числа, которые получились в последнем столбце последнего блока строк, рассчитанного нами ранее. Именно эти числа (4, 7 и 5) будут являться корнями данной системы уравнений. Проверить это можно, подставив их вместо значений X1, X2 и X3 в выражения.
Как видим, в Экселе систему уравнений можно решить целым рядом способов, каждый из которых имеет собственные преимущества и недостатки. Но все эти методы можно условно разделить на две большие группы: матричные и с применением инструмента подбора параметров. В некоторых случаях не всегда матричные методы подходят для решения задачи. В частности тогда, когда определитель матрицы равен нулю. В остальных же случаях пользователь сам волен решать, какой вариант он считает более удобным для себя.
Мы рады, что смогли помочь Вам в решении проблемы.
Задайте свой вопрос в комментариях, подробно расписав суть проблемы. Наши специалисты постараются ответить максимально быстро.
Помогла ли вам эта статья?
Да Нет
В программе Excel имеется обширный инструментарий для решения различных видов уравнений разными методами.
Рассмотрим на примерах некоторые варианты решений.
Решение уравнений методом подбора параметров Excel
Инструмент «Подбор параметра» применяется в ситуации, когда известен результат, но неизвестны аргументы. Excel подбирает значения до тех пор, пока вычисление не даст нужный итог.
Путь к команде: «Данные» — «Работа с данными» — «Анализ «что-если»» — «Подбор параметра».
Рассмотрим на примере решение квадратного уравнения х2 + 3х + 2 = 0. Порядок нахождения корня средствами Excel:
- Введем в ячейку В2 формулу для нахождения значения функции. В качестве аргумента применим ссылку на ячейку В1.
- Открываем меню инструмента «Подбор параметра». В графе «Установить в ячейку» — ссылка на ячейку В2, где находится формула. В поле «Значение» вводим 0. Это то значение, которое нужно получить.
 В графе «Изменяя значение ячейки» — В1. Здесь должен отобразиться отобранный параметр.
В графе «Изменяя значение ячейки» — В1. Здесь должен отобразиться отобранный параметр. - После нажатия ОК отобразится результат подбора. Если нужно его сохранить, вновь нажимаем ОК. В противном случае – «Отмена».
Для подбора параметра программа использует циклический процесс. Чтобы изменить число итераций и погрешность, нужно зайти в параметры Excel. На вкладке «Формулы» установить предельное количество итераций, относительную погрешность. Поставить галочку «включить итеративные вычисления».
Как решить систему уравнений матричным методом в Excel
Дана система уравнений:
- Значения элементов введем в ячейки Excel в виде таблицы.
- Найдем обратную матрицу. Выделим диапазон, куда впоследствии будут помещены элементы матрицы (ориентируемся на количество строк и столбцов в исходной матрице). Открываем список функций (fx). В категории «Математические» находим МОБР. Аргумент – массив ячеек с элементами исходной матрицы.
- Нажимаем ОК – в левом верхнем углу диапазона появляется значение.
 Последовательно жмем кнопку F2 и сочетание клавиш Ctrl + Shift + Enter.
Последовательно жмем кнопку F2 и сочетание клавиш Ctrl + Shift + Enter. - Умножим обратную матрицу Ах-1х на матрицу В (именно в таком порядке следования множителей!). Выделяем диапазон, где впоследствии появятся элементы результирующей матрицы (ориентируемся на число строк и столбцов матрицы В). Открываем диалоговое окно математической функции МУМНОЖ. Первый диапазон – обратная матрица. Второй – матрица В.
- Закрываем окно с аргументами функции нажатием кнопки ОК. Последовательно нажимаем кнопку F2 и комбинацию Ctrl + Shift + Enter.
Получены корни уравнений.
Решение системы уравнений методом Крамера в Excel
Возьмем систему уравнений из предыдущего примера:
Для их решения методом Крамера вычислим определители матриц, полученных заменой одного столбца в матрице А на столбец-матрицу В.
Для расчета определителей используем функцию МОПРЕД. Аргумент – диапазон с соответствующей матрицей.
Рассчитаем также определитель матрицы А (массив – диапазон матрицы А).
Определитель системы больше 0 – решение можно найти по формуле Крамера (Dx / |A|).
Для расчета Х1: =U2/$U$1, где U2 – D1. Для расчета Х2: =U3/$U$1. И т.д. Получим корни уравнений:
Решение систем уравнений методом Гаусса в Excel
Для примера возьмем простейшую систему уравнений:
3а + 2в – 5с = -1
2а – в – 3с = 13
а + 2в – с = 9
Коэффициенты запишем в матрицу А. Свободные члены – в матрицу В.
Для наглядности свободные члены выделим заливкой. Если в первой ячейке матрицы А оказался 0, нужно поменять местами строки, чтобы здесь оказалось отличное от 0 значение.
- Приведем все коэффициенты при а к 0. Кроме первого уравнения. Скопируем значения в первой строке двух матриц в ячейки В6:Е6. В ячейку В7 введем формулу: =B3:Е3-$B$2:$Е$2*(B3/$B$2). Выделим диапазон В7:Е7. Нажмем F2 и сочетание клавиш Ctrl + Shift + Enter. Мы отняли от второй строки первую, умноженную на отношение первых элементов второго и первого уравнения.
- Копируем введенную формулу на 8 и 9 строки.
 Так мы избавились от коэффициентов перед а. Сохранили только первое уравнение.
Так мы избавились от коэффициентов перед а. Сохранили только первое уравнение. - Приведем к 0 коэффициенты перед в в третьем и четвертом уравнении. Копируем строки 6 и 7 (только значения). Переносим их ниже, в строки 10 и 11. Эти данные должны остаться неизменными. В ячейку В12 вводим формулу массива.
- Прямую прогонку по методу Гаусса сделали. В обратном порядке начнем прогонять с последней строки полученной матрицы. Все элементы данной строки нужно разделить на коэффициент при с. Введем в строку формулу массива: {=B12:E12/D12}.
- В строке 15: отнимем от второй строки третью, умноженную на коэффициент при с второй строки ({=(B11:E11-B16:E16*D11)/C11}). В строке 14: от первой строки отнимаем вторую и третью, умноженные на соответствующие коэффициенты ({=(B10:E10-B15:E15*C10-B16:E16*D10)/B10}). В последнем столбце новой матрицы получаем корни уравнения.
Примеры решения уравнений методом итераций в Excel
Вычисления в книге должны быть настроены следующим образом:
Делается это на вкладке «Формулы» в «Параметрах Excel».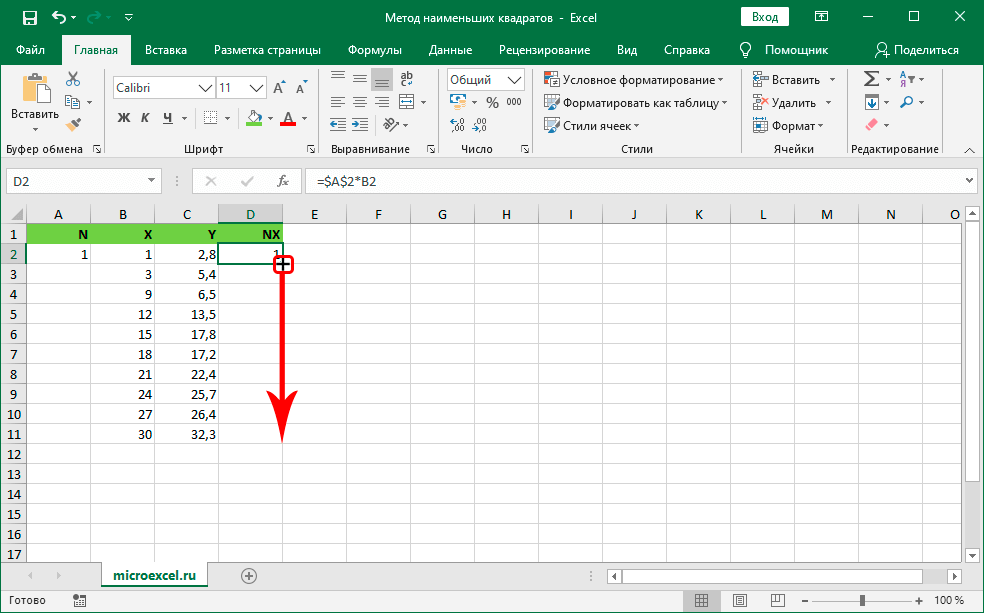 Найдем корень уравнения х – х3 + 1 = 0 (а = 1, b = 2) методом итерации с применением циклических ссылок. Формула:
Найдем корень уравнения х – х3 + 1 = 0 (а = 1, b = 2) методом итерации с применением циклических ссылок. Формула:
Хn+1 = Xn– F (Xn) / M, n = 0, 1, 2, … .
M – максимальное значение производной по модулю. Чтобы найти М, произведем вычисления:
f’ (1) = -2 * f’ (2) = -11.
Полученное значение меньше 0. Поэтому функция будет с противоположным знаком: f (х) = -х + х3 – 1. М = 11.
В ячейку А3 введем значение: а = 1. Точность – три знака после запятой. Для расчета текущего значения х в соседнюю ячейку (В3) введем формулу: =ЕСЛИ(B3=0;A3;B3-(-B3+СТЕПЕНЬ(B3;3)-1/11)).
В ячейке С3 проконтролируем значение f (x): с помощью формулы =B3-СТЕПЕНЬ(B3;3)+1.
Корень уравнения – 1,179. Введем в ячейку А3 значение 2. Получим тот же результат:
Скачать решения уравнений в Excel
Корень на заданном промежутке один.
Задача решения уравнения встает не только перед студентами и школьниками. В Excel можно использовать различные способы выполнения этой задачи. О способе решения путем подбора параметра пойдет речь в этой статье.
О способе решения путем подбора параметра пойдет речь в этой статье.
Нахождение корней нелинейного уравнения с использованием средства
«Подбор параметра» сводится в двум этапам:
- определение приблизительных границ отрезков и количества корней графическим методом;
- подбор на каждом отрезке значения корня, удовлетворяющего заданной точности вычислений.
Примером может служить решение квадратного уравнения, которое в общем виде задается выражением
«Y(x) = ax2 + bx +
c» . Для того, чтобы построенная электронная таблица позволяла бы находить решения подобных уравнений с любыми коэффициентами, лучше вынести коэффициенты в отдельные ячейки, а в формулах для вычисления значений функции использовать ссылки на эти ячейки. Впрочем, это дело вкуса. Можно при составлении формулы использовать значения коэффициентов, а не ссылки на них.
Чтобы оценить примерные границы отрезков и количество корней, можно использовать табличное задание значений функции, т. е. задать несколько значений переменной и вычислить соответствующие значения функции. Опять же, для того, чтобы можно было моделировать расчеты для квадратных уравнений с различными коэффициентами, шаг табулирования лучше задать в отдельной ячейке. Начальное значение переменной можно будет изменять путем ввода в ячейку «
е. задать несколько значений переменной и вычислить соответствующие значения функции. Опять же, для того, чтобы можно было моделировать расчеты для квадратных уравнений с различными коэффициентами, шаг табулирования лучше задать в отдельной ячейке. Начальное значение переменной можно будет изменять путем ввода в ячейку «
А6» . Для вычисления следующего значения в ячейку
«А7» введена формула «
=А6+$
B$4» , т.е. использована абсолютная ссылка на ячейку с шагом табулирования.
Далее с помощью
маркера заполнения формируется ряд формул для вычисления последующих значений переменной, в приведенном примере используется 20 значений.
Вводится формула для вычисления значения функции (для рассматриваемого примера в ячейку «
В6» ) и формируется ряд аналогичных формул для остальных ячеек. В формуле использованы абсолютные ссылки на ячейки с коэффициентами уравнения.
По построенной таблице строится
точечная диаграмма .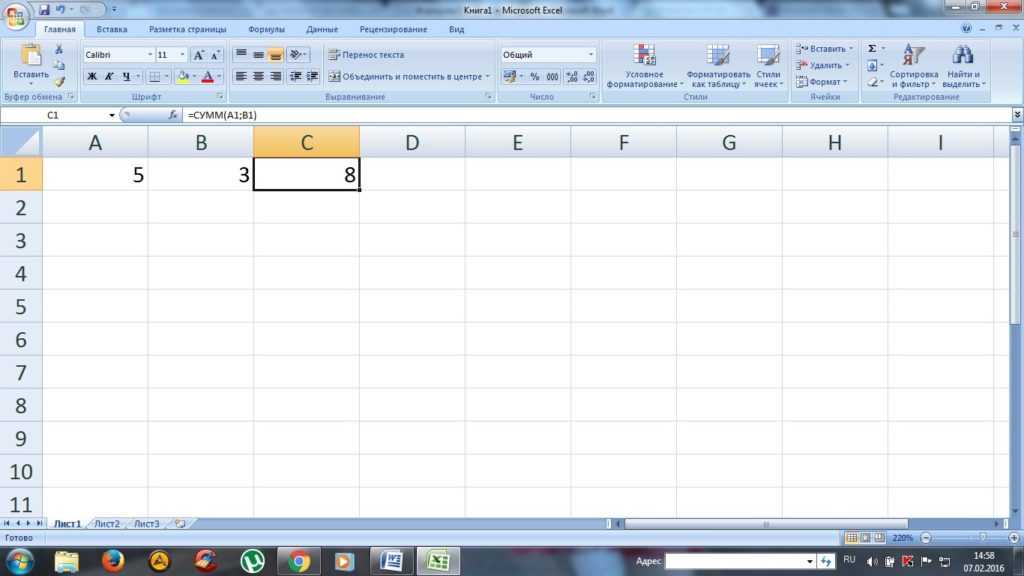
Если начальное значение Х и шаг выбраны неудачно, и на диаграмме нет пересечений с осью абсцисс, то можно ввести другие значения и добиться нужного результата.
Можно было бы найти решение уже на этом шаге, но для этого понадобилось бы гораздо больше ячеек и шаг, равный заданной точности вычислений (0,001). Чтобы не создавать громоздких таблиц, далее используется
«Подбор параметра» из группы
«Прогноз» на вкладке
«Данные» . Предварительно необходимо выделить место под начальные значения переменной (корней в примере два) и соответствующие значения функции. В качестве «
х1» выбирается первое из значений, дающих наиболее близкое к нулю значение функции (в примере 0,5). В
ячейку
L6 введена формула для вычисления функции. В окне подбора параметра необходимо указать для какой ячейки (
L6 ), какое значение (
) нужно получить, и в какой ячейке для этого изменять значения (
К6 ).
Для поиска второго корня необходимо ввести второе из значений, дающих наиболее близкое к нулю значение функции (в примере 9,5), и повторить подбор параметра для ячейки
L9 (в ячейку скопирована формула из ячейки
L6 ).
Предложенное оформление коэффициентов функции в отдельные ячейки позволяет без изменения формул решать другие подобные уравнения.
Подбор параметра имеется и в более ранних версиях программы.
Как использовать поиск цели и решатель Excel для решения неизвестных переменных
Excel — мощный инструмент, когда ваши данные полны. Но было бы неплохо, если бы он мог решить для неизвестных переменных ?
С Goal Seek и надстройкой Solver это возможно. И мы покажем вам, как это сделать. Читайте полное руководство о том, как решить одну ячейку с помощью Goal Seek или более сложное уравнение с помощью Solver.
Как использовать поиск цели в Excel
Поиск цели уже встроен в Excel.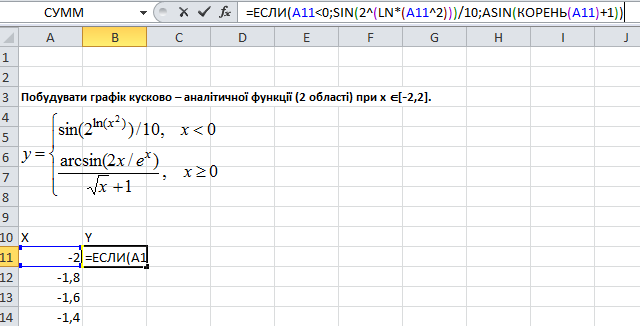 Это под Вкладка «Данные » в меню «Что если анализ» :
Это под Вкладка «Данные » в меню «Что если анализ» :
В этом примере мы будем использовать очень простой набор чисел. У нас есть данные о продажах за три квартала и цель на год. Мы можем использовать поиск цели, чтобы выяснить, какие числа должны быть в Q4, чтобы достичь цели.
Как видите, текущий объем продаж составляет 114 706 единиц. Если мы хотим продать 250 000 к концу года, сколько нам нужно продать в четвертом квартале? Поиск цели Excel расскажет нам.
Вот как использовать поиск цели, шаг за шагом:
- Щелкните Данные > Анализ «что, если» > Поиск цели . Появится окно поиска цели.
- Поместите «равно» часть вашего уравнения в поле Установить ячейку . Это число, которое Excel попытается оптимизировать. В нашем случае это промежуточная сумма продаж в ячейке A5.
- Введите значение цели в поле До значения . Мы ищем в общей сложности 250 000 проданных единиц, поэтому мы поместим «250 000» в это поле.

- Сообщите Excel, какую переменную нужно найти в , изменив поле ячейки . Мы хотим увидеть, какими должны быть наши продажи в четвертом квартале. Итак, мы скажем Excel решить для ячейки D2. Когда он будет готов к работе, он будет выглядеть так:
- Нажмите OK , чтобы решить свою цель. Когда все выглядит хорошо, просто нажмите OK . Excel сообщит вам, когда Goal Seek найдет решение.
- Нажмите OK еще раз, и вы увидите значение, которое решает ваше уравнение в ячейке, которую вы выбрали для Путем изменения ячейки .
В нашем случае решение составляет 135 294 единицы. Конечно, мы могли бы просто найти это, вычтя промежуточную сумму из годовой цели. Но поиск цели также можно использовать в ячейке, в которой уже есть данные . И это более полезно.
Обратите внимание, что Excel перезаписывает наши предыдущие данные. Это хорошая идея запустить поиск цели на копии ваших данных . Также неплохо отметить в скопированных данных, что они были сгенерированы с помощью поиска цели. Вы не хотите путать его с текущими, точными данными.
Также неплохо отметить в скопированных данных, что они были сгенерированы с помощью поиска цели. Вы не хотите путать его с текущими, точными данными.
Итак, поиск цели — полезная функция Excel, но она не так уж впечатляет. Вы можете использовать его только в одной ячейке за раз. Если вы хотите использовать поиск цели Excel одновременно в нескольких ячейках, вам понадобится гораздо более мощный инструмент. К счастью, один из таких инструментов поставляется вместе с Excel. Давайте посмотрим на надстройку Solver.
Что делает решатель Excel?
Короче говоря, Solver похож на многомерную версию Goal Seek . Если вам интересно, как использовать поиск цели в Excel для нескольких ячеек одновременно, вот оно. Он берет одну целевую переменную и регулирует ряд других переменных, пока не получит желаемый ответ.
Он может найти максимальное значение числа, минимальное значение числа или точное число. И он работает в пределах ограничений, поэтому, если одна переменная не может быть изменена или может изменяться только в указанном диапазоне, Solver примет это во внимание.
Это отличный способ найти несколько неизвестных переменных в Excel. Но найти и использовать его не так просто. Давайте взглянем на загрузку надстройки «Поиск решения», а затем перейдем к тому, как использовать «Поиск решения» в текущей версии Microsoft 365 Excel.
Как загрузить надстройку Solver
Excel не имеет Решателя по умолчанию. Это надстройка, поэтому сначала ее нужно загрузить. К счастью, он уже есть на вашем компьютере.
Перейдите к Файл > (Дополнительно… >) Параметры > Надстройки . Затем нажмите Перейти рядом с Управление: надстройки Excel .
Если в этом раскрывающемся списке указано что-то отличное от «Надстройки Excel», вам нужно изменить его:
В появившемся окне вы увидите несколько вариантов. Убедитесь, что поле рядом с Надстройка Solver проверена и нажала OK .
Теперь вы увидите кнопку Solver в группе Analysis на вкладке Data :
Если вы уже использовали пакет инструментов анализа данных, вы увидите кнопку Анализ данных.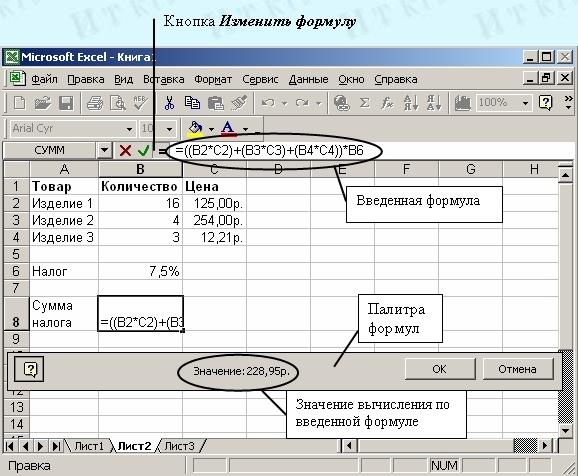 Если нет, Solver появится сам по себе.
Если нет, Solver появится сам по себе.
Теперь, когда вы загрузили надстройку, давайте посмотрим, как ее использовать.
Как использовать решатель в Excel
Любое действие Решателя состоит из трех частей: цель, переменные ячейки и ограничения. Мы пройдемся по каждому из шагов.
- Нажмите Данные > Решатель . Ниже вы увидите окно Solver Parameters. (Если вы не видите кнопку «Поиск решения», см. предыдущий раздел о том, как загрузить надстройку «Поиск решения».)
- Установите цель своей ячейки и сообщите Excel свою цель. Цель находится в верхней части окна Решателя и состоит из двух частей: ячейка цели и выбор максимизации, минимизации или конкретного значения. Если вы выберете Max , Excel настроит ваши переменные, чтобы получить максимально возможное число в целевой ячейке. Мин. наоборот: Решатель минимизирует число цели. Значение позволяет указать конкретное число, которое будет искать Solver.

- Выберите ячейки переменных, которые Excel может изменить. Ячейки переменных устанавливаются с помощью поля By Changeable Variable Cells . Щелкните стрелку рядом с полем, затем щелкните и перетащите, чтобы выбрать ячейки, с которыми должен работать Solver. Обратите внимание, что это все ячейки , которые могут варьироваться. Если вы не хотите, чтобы ячейка изменялась, не выбирайте ее.
- Установите ограничения для нескольких или отдельных переменных. Наконец, мы подошли к ограничениям. Вот где Solver действительно силен. Вместо того, чтобы изменять любую из переменных ячеек на любое желаемое число, вы можете указать ограничения, которые должны быть соблюдены. Дополнительные сведения см. в разделе о том, как установить ограничения ниже.
- Когда вся эта информация будет на месте, нажмите Решить , чтобы получить ответ. Excel обновит ваши данные, включив в них новые переменные (поэтому мы рекомендуем сначала создать копию ваших данных).

Вы также можете создавать отчеты, которые мы кратко рассмотрим в нашем примере с Солвером ниже.
Как установить ограничения в Solver
Вы можете указать Excel, что одна переменная должна быть больше 200. При попытке использовать разные значения переменных Excel не будет опускаться ниже 201 с этой конкретной переменной.
Чтобы добавить ограничение, нажмите кнопку Добавить рядом со списком ограничений. Вы получите новое окно. Выберите ячейку (или ячейки) для ограничения в Cell Reference , затем выберите оператора.
Доступные операторы:
- <= (меньше или равен)
- = (равна)
- => (больше или равна)
- int (должен быть цетком)
- (должно быть либо 1, либо 0)
- AllDifferent
AllDifferent немного сбивает с толку.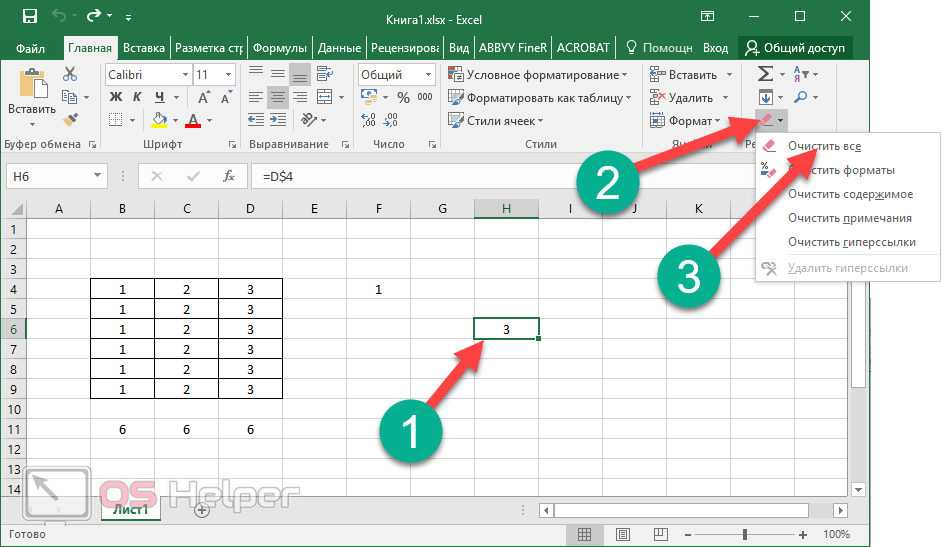 Он указывает, что каждая ячейка в диапазоне, который вы выбираете для Ссылка на ячейку должна быть другим номером. Но также указывается, что они должны быть между 1 и количеством ячеек. Итак, если у вас есть три ячейки, вы получите числа 1, 2 и 3 (но не обязательно в таком порядке)
Он указывает, что каждая ячейка в диапазоне, который вы выбираете для Ссылка на ячейку должна быть другим номером. Но также указывается, что они должны быть между 1 и количеством ячеек. Итак, если у вас есть три ячейки, вы получите числа 1, 2 и 3 (но не обязательно в таком порядке)
.
Наконец, добавьте значение ограничения.
Важно помнить, что вы можете выбрать несколько ячеек для ссылки на ячейку. Например, если вы хотите, чтобы шесть переменных имели значения больше 10, вы можете выбрать их все и указать Solver, что они должны быть больше или равны 11. Вам не нужно добавлять ограничение для каждой ячейки.
Вы также можете установить флажок в главном окне Решателя, чтобы убедиться, что все значения, для которых вы не указали ограничения, неотрицательны. Если вы хотите, чтобы ваши переменные стали отрицательными, снимите этот флажок.
Пример решателя
Чтобы увидеть, как все это работает, мы воспользуемся надстройкой Solver для быстрого расчета. Вот данные, с которых мы начинаем:
Вот данные, с которых мы начинаем:
В ней у нас есть пять разных заданий, каждое из которых оплачивается по разным ставкам. У нас также есть количество часов, которое теоретический рабочий отработал на каждой из этих работ в данную неделю. Мы можем использовать надстройку Solver, чтобы узнать, как максимизировать общую оплату, удерживая определенные переменные в некоторых ограничениях.
Вот ограничения, которые мы будем использовать:
- Нет заданий может быть менее четырех часов.
- Задание 4 должно быть больше 12 часов .
- Работа 5 должна быть менее одиннадцати часов .
- Общее количество отработанных часов должно быть равно 40 .
Может быть полезно записать ваши ограничения перед использованием Solver.
Вот как мы настроили это в Солвере:
Во-первых, обратите внимание, что Я создал копию таблицы , поэтому мы не перезаписываем исходную таблицу, которая содержит наши текущие часы работы.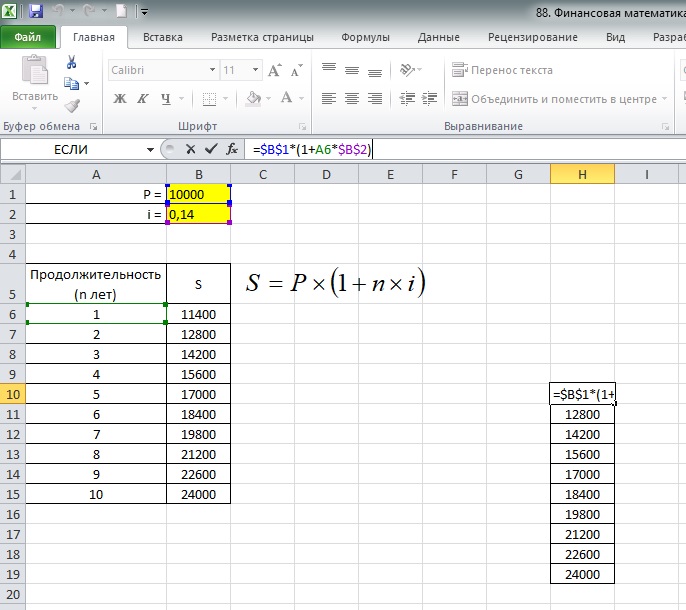
И, во-вторых, обратите внимание, что значения в ограничениях больше и меньше на единицу больше или меньше , чем то, что я упомянул выше. Это потому, что нет вариантов больше или меньше. Есть только больше-или-равно и меньше-или-равно.
Нажмем Решим и посмотрим, что получится.
Solver нашел решение! Как вы можете видеть в левой части окна выше, наша прибыль увеличилась на 130 долларов. И все ограничения соблюдены.
Чтобы сохранить новые значения, установите флажок Keep Solver Solution и нажмите OK .
Если вам нужна дополнительная информация, вы можете выбрать отчет в правой части окна. Выберите все отчеты, которые вы хотите, сообщите Excel, хотите ли вы, чтобы они были выделены в общих чертах (я рекомендую это), и нажмите OK .
Отчеты создаются на новых листах в вашей рабочей книге и содержат информацию о процессе, через который надстройка «Поиск решения» прошла, чтобы получить ваш ответ.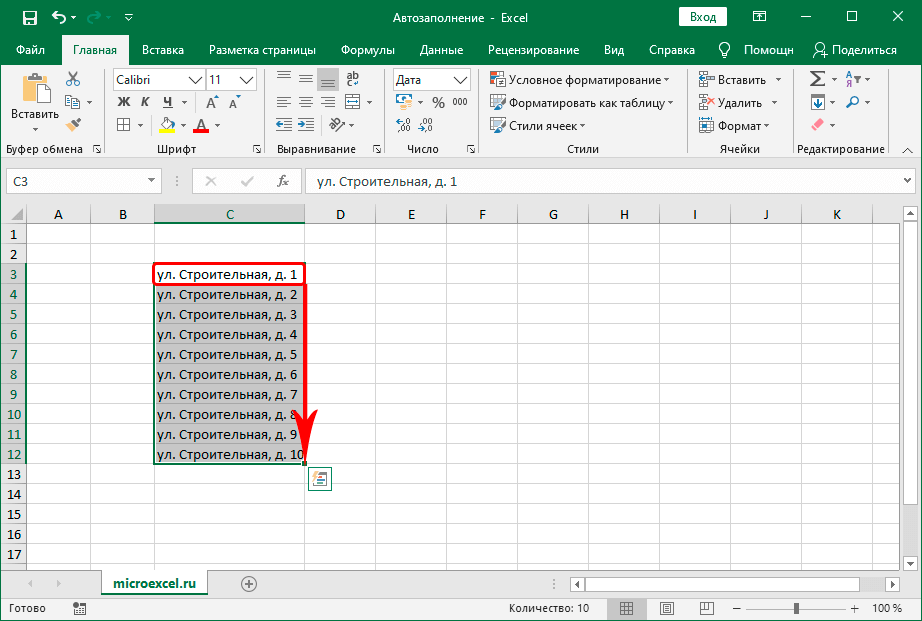
В нашем случае отчеты не очень интересные, да и интересной информации там не много. Но если вы запустите более сложное уравнение Solver, вы можете найти полезную отчетную информацию в этих новых рабочих листах. Просто нажмите кнопку + сбоку от любого отчета, чтобы получить дополнительную информацию:
Дополнительные параметры решателя
Если вы мало разбираетесь в статистике, вы можете игнорировать расширенные параметры Солвера и просто запустить его как есть. Но если вы выполняете большие и сложные вычисления, вы можете изучить их.
Самый очевидный метод решения:
Вы можете выбрать между GRG Nonlinear, Simplex LP и Evolutionary. Excel предоставляет простое объяснение того, когда вы должны использовать каждый из них. Лучшее объяснение требует некоторого знания статистики Excel и регрессии.
Чтобы настроить дополнительные параметры, просто нажмите кнопку Опции . Вы можете сообщить Excel об оптимальности целых чисел, установить временные ограничения вычислений (полезно для массивных наборов данных) и настроить методы решения GRG и Evolutionary для выполнения своих вычислений.
Опять же, если вы не знаете, что это означает, не беспокойтесь об этом. Если вы хотите узнать больше о том, какой метод решения использовать, у Engineer Excel есть хорошая статья, в которой он изложен для вас. Если вам нужна максимальная точность, Evolutionary, вероятно, является хорошим выбором. Просто знайте, что это займет много времени.
Поиск цели и решение: выход Excel на новый уровень
Теперь, когда вы освоились с основами решения неизвестных переменных в Excel, перед вами открыт совершенно новый мир вычислений в электронных таблицах. Goal Seek может помочь вам сэкономить время, выполняя некоторые вычисления быстрее, а Solver значительно расширяет вычислительные возможности Excel.
Нужно просто привыкнуть к ним. Чем больше вы их используете, тем полезнее они будут становиться.
Решить уравнение в Excel | Как решить уравнение с помощью надстройки Solver
Решение уравнения в Excel (оглавление)
- Обзор решения уравнения в Excel
- Как добавить надстройку Solver?
- Пример решения уравнений с помощью надстройки Solver
Excel во многом помогает нам, упрощая и упрощая задачу. 9Надстройка 0003 Solver Инструмент необходим для выполнения или решения уравнений в Excel. Иногда нам нужно выполнить или провести обратные вычисления, где нам нужно вычислить одну или две переменные, чтобы получить желаемые конечные результаты.
9Надстройка 0003 Solver Инструмент необходим для выполнения или решения уравнений в Excel. Иногда нам нужно выполнить или провести обратные вычисления, где нам нужно вычислить одну или две переменные, чтобы получить желаемые конечные результаты.
Пример: Для получения дополнительных 10%, сколько единиц необходимо продать или какие точные оценки необходимо получить в последнем семестре выпускных экзаменов, чтобы получить отличие.
Вышеупомянутый расчет или уравнения могут быть рассчитаны с помощью надстройки Solver с определенными критериями.
Определение уравнения решения в Excel
Используется для определения оптимального значения целевой ячейки путем изменения значений в ячейках, используемых для вычисления целевой ячейки.
Содержит следующие параметры.
- Цель
- Переменные
- Ограничения
- Формула для расчета
Как добавить надстройку Solver?
Давайте посмотрим, как добавить надстройку решателя в Excel. Расчет или уравнения могут быть рассчитаны с помощью надстройки Solver с определенными критериями.
Расчет или уравнения могут быть рассчитаны с помощью надстройки Solver с определенными критериями.
Чтобы добавить надстройку Solver, выполните следующую процедуру:
- Нажмите кнопку «Файл» или кнопку Office; затем вам нужно нажать «Параметры Excel».
- Теперь появится диалоговое окно «Параметры Excel»; в разделе «Надстройки» выберите «Надстройка Solver» в списке неактивных надстроек приложения и « Go. »
- Появится окно надстроек, где вы можете увидеть список активных надстроек. Отметьте надстройку Solver и нажмите кнопку «ОК».
Теперь вы можете заметить, что надстройка Solver была добавлена на лист Excel как Solver на вкладке «Данные» в крайней правой части.
Пример решения уравнений с помощью надстройки «Решатель»
Расчет значений переменных для максимизации прибыли в % с помощью надстройки «Решатель».
Вы можете скачать этот шаблон Excel для решения уравнения здесь — Шаблон Excel для решения уравнения
В приведенной выше таблице ежемесячные данные о продажах по цене за единицу, содержащие стоимость или самую низкую цену за единицу и цену продажи за единицу для клиентов.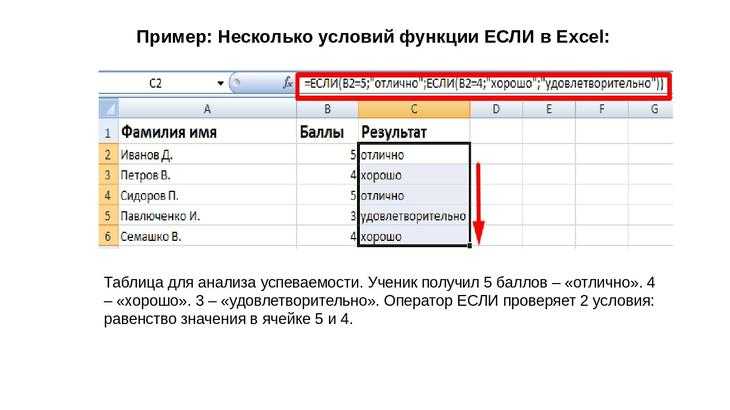 . Теперь у меня есть апрель и май с процентной прибылью на каждую единицу, то есть 13,33% и 15,38% соответственно.
. Теперь у меня есть апрель и май с процентной прибылью на каждую единицу, то есть 13,33% и 15,38% соответственно.
Здесь B4 и C4 — процентная прибыль за апрель и май 2019 года, которая рассчитывается с помощью приведенной ниже формулы.
Формула для определения P ercentage Прибыль :
((Продажная цена за единицу – Цена по складу за единицу)/ Цена по складу за единицу) *100
Переменные и C3 (B2, C3) ): Здесь переменными являются стоимость или самая низкая цена за единицу и цена продажи за единицу для клиентов, которая продолжает меняться из месяца в месяц.
Цели и ограничения
Теперь моя цель — довести процентную прибыль (%) на единицу до 20%. Итак, для этого мне нужно узнать стоимость или самую низкую цену за единицу и цену продажи за единицу для клиентов, необходимых для получения прибыли в размере 20%.
- Целевая ячейка : D4 (прибыль %) должен дать 20% прибыли
- Переменные ячейки : C2 (Себестоимость или самая низкая цена за единицу) и C3 (Продажная цена за единицу для клиентов)
- Ограничения: D2 должно быть >= 16 000, а D3 должно быть <= 20 000
Формула для определения P ercentage Прибыль :
((Продажная цена за единицу – Цена на складе за единицу)/ Цена на складе за единицу) *100
т. е. ((D3-D2)/D2) *100
е. ((D3-D2)/D2) *100
Перед использованием надстройки решателя нам необходимо ввести формулу калькулятора прибыли ((D3-D2)/D2) *100 в целевую ячейку (D4), чтобы рассчитать 20% прибыли.
Это важная информация, необходимая для решения любого уравнения с помощью надстройки Solver в Excel. Теперь выберите ячейку D4, и мне нужно запустить надстройку Solver, щелкнув вкладку Data и выбрав Solver.
После выбора решателя появится окно параметров решателя, в котором необходимо указать «Целевая ячейка» как ссылку на ячейку «D4» в текстовом поле «Установить цель» и выбрать переключатель «Значение», в тексте его поле устанавливает целевую прибыль в размере 20 %
В ячейках «Изменяя переменные» выберите диапазон ячеек D2 (Стоимость или самая низкая цена за единицу) и D3 (Цена продажи за единицу для клиентов), где он указан как $D$2:$ D$3 в текстовом поле.
После добавления изменяющегося диапазона ячеек нам нужно добавить ограничения; он добавляется нажатием кнопки «Добавить» под субъектом ограничений.
Теперь добавляется первый параметр ограничений путем ввода ссылки на ячейку и значения ограничения, т. е. себестоимости или максимальной цены за единицу, которая больше или равна 16 000 ( >= 16000)
Теперь это отображается в поле «При условии соблюдения ограничений», снова нам нужно нажать «Добавить», чтобы добавить еще одно ограничение, т. Е. Цена продажи за единицу для клиентов, она добавляется путем ввода ссылка на ячейку и значение ограничения, которое меньше или равно 20 000 (<=20000)
Теперь мы добавили все параметры; просто нам нужно нажать на решить.
Он спросит, хотите ли вы сохранить решение решателя вместе с исходными значениями; вы можете выбрать эти параметры в зависимости от ваших требований; здесь, в этом сценарии, я выбрал Keep Solver Solution и нажимаю кнопку «ОК».
Теперь вы увидите изменение значения в ячейке D2 (Стоимость или самая низкая цена за единицу) и D3 (Цена продажи за единицу покупателям) на 16000 и 19200 соответственно, чтобы получить 20% прибыли.

 В качестве стартовых можно взять любые значения, например, нули или единицы — роли не играет. Для удобства, кстати, этим ячейкам можно дать имена, назвав их именами переменных x и y, — для этого выделите диапазон C9:C10 и выберите команду Формулы — Создать из выделенного — Слева (Formulas — Create from selection — Left column).
В качестве стартовых можно взять любые значения, например, нули или единицы — роли не играет. Для удобства, кстати, этим ячейкам можно дать имена, назвав их именами переменных x и y, — для этого выделите диапазон C9:C10 и выберите команду Формулы — Создать из выделенного — Слева (Formulas — Create from selection — Left column). 

 Для этих целей устанавливаем курсор в это поле. Затем зажимаем левую кнопку мыши и выделяем область на листе, в которой находится матрица. Как видим, данные о координатах размещения автоматически заносятся в поле окна. После того, как эта задача выполнена, наиболее очевидным было бы нажать на кнопку «OK», но не стоит торопиться. Дело в том, что нажатие на эту кнопку является равнозначным применению команды Enter. Но при работе с массивами после завершения ввода формулы следует не кликать по кнопке Enter, а произвести набор сочетания клавиш Ctrl+Shift+Enter. Выполняем эту операцию.
Для этих целей устанавливаем курсор в это поле. Затем зажимаем левую кнопку мыши и выделяем область на листе, в которой находится матрица. Как видим, данные о координатах размещения автоматически заносятся в поле окна. После того, как эта задача выполнена, наиболее очевидным было бы нажать на кнопку «OK», но не стоит торопиться. Дело в том, что нажатие на эту кнопку является равнозначным применению команды Enter. Но при работе с массивами после завершения ввода формулы следует не кликать по кнопке Enter, а произвести набор сочетания клавиш Ctrl+Shift+Enter. Выполняем эту операцию. Далее опять запускаем Мастер функций, нажав значок «Вставить функцию».
Далее опять запускаем Мастер функций, нажав значок «Вставить функцию». 2+4*x-132
2+4*x-132  В нашем случае, как видим, x будет равен 6.
В нашем случае, как видим, x будет равен 6. Для расчета этого значения в Экселе опять имеется отдельная функция – МОПРЕД. Синтаксис данного оператора следующий:
Для расчета этого значения в Экселе опять имеется отдельная функция – МОПРЕД. Синтаксис данного оператора следующий:

 В нашем случае формула будет иметь следующий вид:
В нашем случае формула будет иметь следующий вид: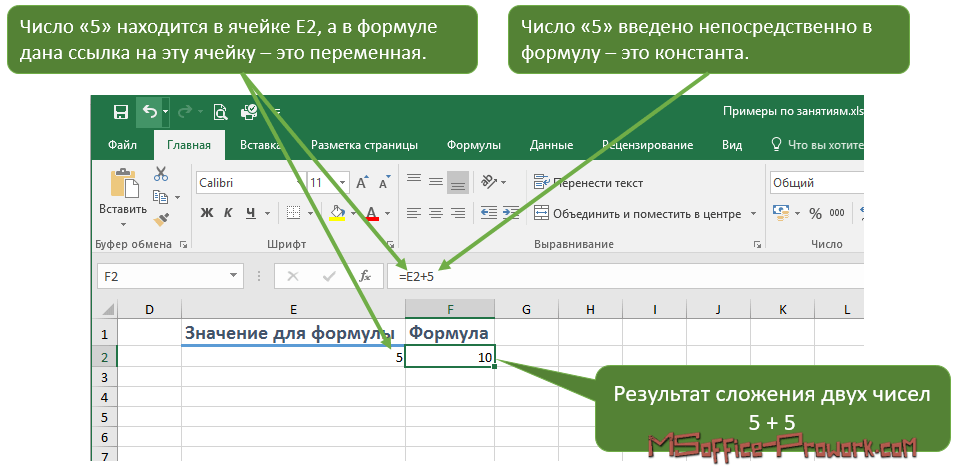
 В графе «Изменяя значение ячейки» — В1. Здесь должен отобразиться отобранный параметр.
В графе «Изменяя значение ячейки» — В1. Здесь должен отобразиться отобранный параметр.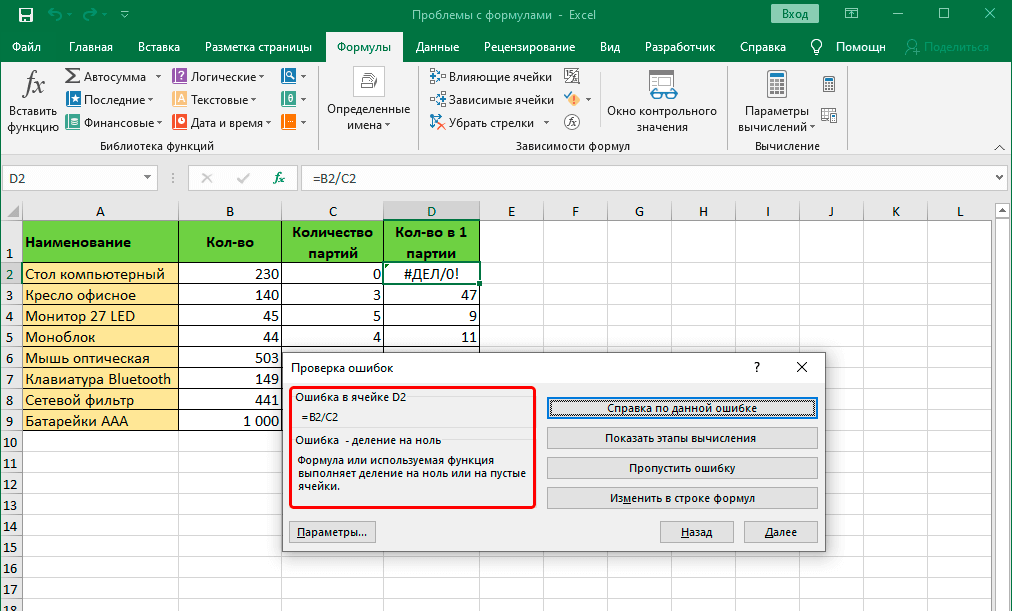 Последовательно жмем кнопку F2 и сочетание клавиш Ctrl + Shift + Enter.
Последовательно жмем кнопку F2 и сочетание клавиш Ctrl + Shift + Enter.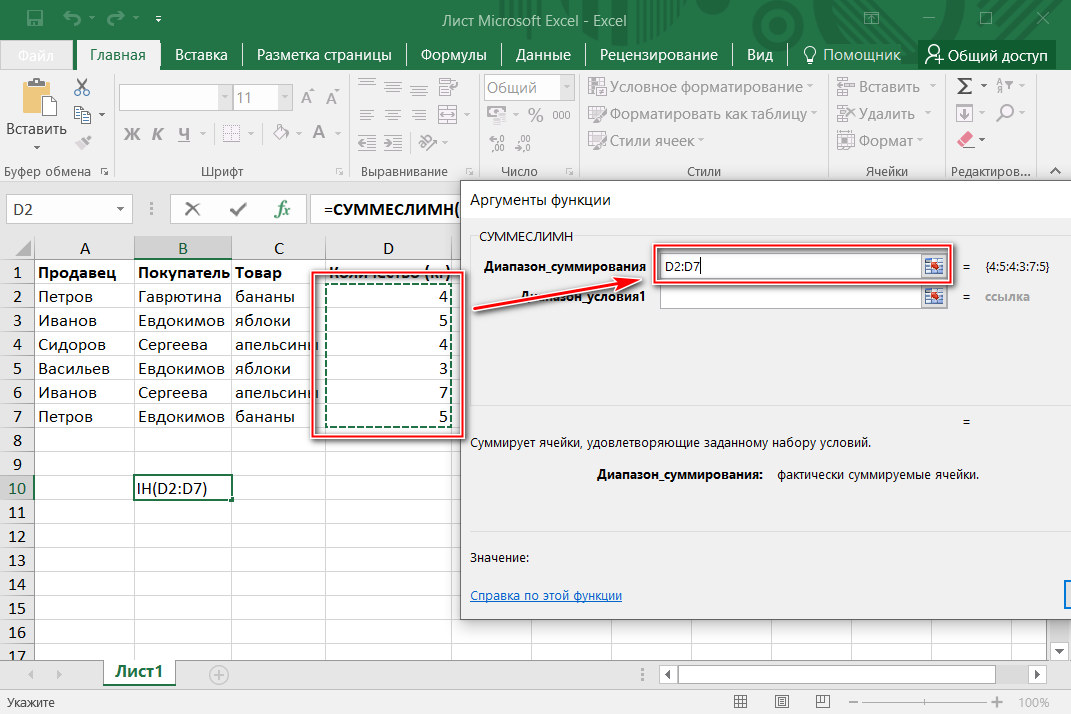 Так мы избавились от коэффициентов перед а. Сохранили только первое уравнение.
Так мы избавились от коэффициентов перед а. Сохранили только первое уравнение.


