Формулы проведения: Формулы приведения: таблица, примеры, правила

Содержание

Формулы приведения: таблица, примеры, правила

Поможем понять и полюбить математику

Начать учиться

Из этой статьи вы узнаете, как привести тригонометрические функции огромных аргументов к функциям аргумента из промежутка [0; π/2]. А еще — как в этом занятии поможет лошадка и кому она кивает. 🐴

Вы наверняка помните значения тригонометрических функций основных аргументов:

Но что делать, если в задаче просят вычислить ? В этом и других случаях, когда из огромного аргумента нам нужно получить аргумент в пределе от 0 до 90 градусов, работают формулы приведения.

Всего формул приведения тридцать две штуки, но прежде чем мы перейдем к формулам, давайте договоримся, что точку тригонометрической окружности, отвечающую углу , где n — целое число, мы будем называть опорной точкой.

Список формул приведения

Формулы приведения c опорной точкой (случай n = 1):

  • ;

  • ;

  • ;

  • ;

  • ;

  • ;

  • ;

  • .

Формулы приведения c опорной точкой (случай n = 2):

  • ;

  • ;

  • ;

  • ;

  • ;

  • ;

  • ;

  • .

Формулы приведения c опорной точкой (случай n = 3):

  • ;

  • ;

  • ;

  • ;

  • ;

  • ;

  • ;

  • .

Формулы приведения c опорной точкой (случай n = 4):

  • ;

  • ;

  • ;

  • ;

  • ;

  • ;

  • ;

  • .

Реши домашку по математике на 5.

Подробные решения помогут разобраться в самой сложной теме.

Доказательство формул

Чтобы убедиться, что формулы рабочие, рассмотрим примеры доказательств нескольких из них.

Для этого нам нужно будет вспомнить формулы сложения для синуса и косинуса:

  • ;

  • .

Формула приведения с синусом

Разберем первый пример формулы приведения с синусом: . Нужно доказать, что левая часть равна правой.

По формуле синуса суммы представим левую часть выражения:

Вычислим и в получившемся выражении:

Таким образом, , что и требовалось доказать.

Формула приведения с косинусом

Рассмотрим также пример формулы приведения с косинусом и докажем ее:

Аналогично распишем левую часть по формуле косинуса суммы:

Вычислим и

Следовательно, , что и требовалось доказать.

Формула приведения с тангенсом

Чтобы доказать формулу приведения с тангенсом, нужно вспомнить, что тангенс — это отношение синуса к косинусу. Тогда для доказательства нужно лишь дважды использовать формулы сложения — попробуйте сами на формуле и сравните с примером.

При желании таким образом вы сможете доказать справедливость всех формул.

Таблица формул приведения

Нередко можно встретить такой вариант оформления формул приведения — в виде таблицы.

Для того чтобы воспользоваться этой таблицей, выберите строку с нужной функцией и столбец с необходимым аргументом — на их пересечении вы узнаете ответ.

Например, нужно упростить . говорит нам о том, что нужно выбрать первую строку, указывает на шестую колонку. На их пересечении нашли ответ: . Значит,

Маленькую распечатанную таблицу формул приведения тригонометрических функций удобно иметь в пенале на случай неожиданных контрольных.

Как запомнить формулы приведения

Одно дело — воспользоваться формулами, а совсем другое — выучить их. Знать наизусть все формулы приведения или всю таблицу — дело нелегкое и, к счастью, абсолютно ненужное.

Поэтому познакомимся с мнемоническим алгоритмом:

  1. Представьте аргумент в виде , где n — целое число, а — острый угол, то есть принадлежит отрезку

  2. Изобразите (на листе или мысленно) на единичной окружности данный угол.

  3. С помощью окружности определите знак исходной функции. Полученная функция в правой части будет иметь такой же знак.

    Напоминаю знаки тригонометрических функций во всех четвертях тригонометрической окружности:

  4. Если в аргументе у опорной точки n — нечетное число, то исходную функцию замените на кофункцию, то есть на противоположную функцию (синус меняется на косинус, тангенс — на котангенс, и наоборот).

    Если в аргументе у опорной точки n — четное число, то функция не меняется.

Вот с этим пунктом изменения или сохранения функции возникает постоянная путаница. А запомнить поможет «правило лошадки».

Правило лошадки 🐴

Когда вы во втором шаге изобразили на единичной окружности угол, обратите внимание на положение опорной точки. Если она располагается на вертикальной оси, то при вопросе «Меняется ли функция?» лошадка кивает головой вверх-вниз и отвечает: «Да». Если опорная точка располагается на горизонтальной оси, то лошадка мотает головой влево-вправо и отвечает: «Нет, функция не меняется».

Таким образом, формулы приведения — это тригонометрические тождества вида

Задание 1

Найдите значение выражения

Вы видите, что каждое слагаемое выражения — это формула приведения тригонометрической функции. Упростим их по отдельности.

  1. Сначала нужно представить аргумент в виде , где n — целое число, а — острый угол. Здесь этот шаг уже выполнен, поэтому пропускаем его.

  2. Далее изображаем данный угол на тригонометрической окружности:

  3. Определяем знак исходной функции, то есть синуса. Синус этого угла принимает положительные значения.

  4. В конце определяем, меняется ли функция. В этом нам поможет «правило лошадки»: опорная точка лежит на горизонтальной оси, значит, функция не меняется на кофункцию, то есть синус не меняется на косинус.

Значит, .

Приведем аналогичные рассуждения для всех слагаемых в выражении.

  1. Аргумент уже представлен в виде , где n — целое число, а — острый угол.

  2. Косинус во второй четверти тригонометрической окружности принимает отрицательные значения.

  3. Опорная точка лежит на вертикальной оси — это случай, когда косинус меняется на синус.

Значит, .

  1. Аргумент уже представлен в виде , где n — целое число, а — острый угол.

  2. Косинус в третьей четверти тригонометрической окружности принимает отрицательные значения.

  3. Опорная точка лежит на вертикальной оси — это случай, когда косинус меняется на синус.

Значит, .

А теперь запишем преобразованные выражения в наше исходное и упростим:

Обратите внимание, к какому простому виду удалось привести это сложное, на первый взгляд, выражение.

Задание 2

До этого момента мы говорили о формулах приведения тригонометрических функций углов, выраженных в радианах. Однако мы понимаем, что градусы и радианы — это разные способы представления одних и тех же углов или аргументов, поэтому тригонометрические формулы приведения работают и для выражений с градусами.

Разберем на примере: найдите значение выражения .

В этом случае важно заметить, что , а значит, одну из функций, например , можно представить в виде , то есть в виде, необходимом для использования формулы приведения.

Так как первый шаг выполнен, то продолжаем идти по алгоритму.

Косинус в первой четверти тригонометрической окружности принимает положительные значения.

Опорная точка лежит на вертикальной оси, поэтому косинус меняется на синус.

Значит,

Запишем преобразованные выражения в наше исходное и упростим:

Формулы приведения в тригонометрии занимают второе место по важности и частоте использования после основного тригонометрического тождества, так что осваивайте теоретические материалы, практикуйтесь на задачках, а за другими полезными формулами и самыми хитрыми заданиями приходите на онлайн-курсы математики для детей в Skysmart.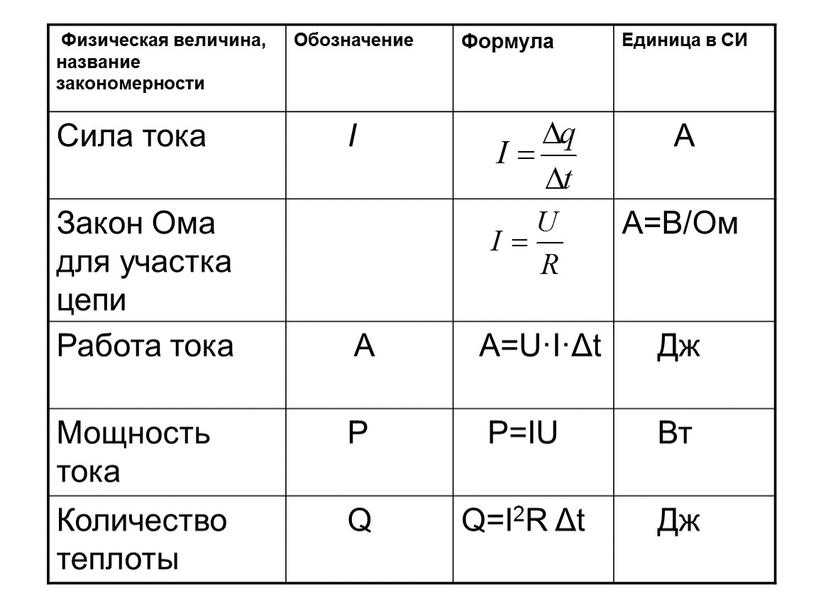

Шпаргалки для родителей по математике

Все формулы по математике под рукой

Кристина Тоскина

К предыдущей статье

Уравнение касательной к графику функции

К следующей статье

207.4K

Логарифмы

Получите план обучения, который поможет понять и полюбить математику

На вводном уроке с методистом

  1. Выявим пробелы в знаниях и дадим советы по обучению

  2. Расскажем, как проходят занятия

  3. Подберём курс

Формулы приведения. Как быстро получить любую формулу приведения



Формулы приведения разработаны для углов, представленных в одном из следующих видов: \(\frac{\pi}{2}+a\), \(\frac{\pi}{2}-a\), \(π+a\), \(π-a\), \(\frac{3\pi}{2}+a\), \(\frac{3\pi}{2}-a\), \(2π+a\) и \(2π-a\). °-a\). К счастью, учить наизусть формулы привидения вам не придется, потому что есть легкий и надежный способ вывести нужную за пару секунд.

Как быстро получить любую формулу приведения


Для начала обратите внимание, что все формулы имеют похожий вид:



Здесь нужно пояснить термин «кофункция» — это та же самая функция с добавлением или убиранием приставки «ко-». То есть, для синуса кофункцией будет косинус, а для косинуса – синус. С тангенсом и котангенсом – аналогично.


Функция:                Кофункция:

\(sin⁡\) \(a\)          \(→\)            \(cos⁡\) \(a\)

\(cos⁡\) \(a\)          \(→\)             \(sin⁡\) \(a\)

\(tg⁡\) \(a\)            \(→\)            \(ctg\) \(a\)

\(ctg⁡\) \(a\)          \(→\)             \(tg\) \(a\)


Таким образом, например, синус при применении этих формул никогда не поменяется на тангенс
или котангенс, он либо останется синусом, либо превратиться в косинус. °}}=\)


 


В числителе и знаменателе получились одинаковые косинусы. Сокращаем их.



\(= 18\)


 


Записываем ответ



Ответ:  \(18\)


Пример. Найдите значение выражения \(\frac{3 \sin{⁡(\pi-a)}-\cos(\frac{\pi}{2}+a) }{\cos⁡ {(\frac{3\pi}{2}-a)}}\)

Решение:








\(\frac{3 \sin{⁡(\pi-a)}-\cos(\frac{\pi}{2}+a) }{\cos⁡ {(\frac{3\pi}{2}-a)}}=\)



Рассмотрим первое слагаемое числителя: \(\sin⁡(π-a)\). Воспользуемся формулами приведения, выведя ее самостоятельно:

  • \((π-a)\) это вторая четверть, а синус во второй четверти положителен. Значит, знак будет плюс;

  • \(π\) это точка «горизонтальная», то есть мотаем головой, значит функция остается той же.


Таким образом, \(\sin⁡(π-a)=\sin⁡a\) 


\(=\frac{3 \sin{⁡a}-\cos(\frac{\pi}{2}+a) }{\cos⁡ {(\frac{3\pi}{2}-a)}}=\)


 

Второе слагаемое числителя: \(\cos⁡{(\frac{π}{2} + a)}\):

  • \((\frac{π}{2} + a)\) это опять вторая четверть, а косинус во второй четверти отрицателен. Значит, знак будет минус.

  • \(\frac{π}{2}\) это точка «вертикальная», то есть киваем, значит, функция меняется на кофункцию – синус.


Таким образом, \(\cos{⁡(\frac{π}{2} + a)}=-\sin⁡a\)


\(=\frac{3 \sin{⁡a}-(-\sin{a}) }{\cos⁡ {(\frac{3\pi}{2}-a)}}=\)


 


Теперь знаменатель: \(\cos⁡(\frac{3π}{2} — a)\). Его мы разобрали выше, он равен минус синусу. \(\cos⁡(\frac{3π}{2} — a)=-\sin{⁡a}\)


\(=\frac{3 \sin{⁡a}-(-\sin{a}) }{-\sin⁡ {a}}=\)


 


Раскрываем скобки и приводим подобные слагаемые.


\(=\frac{3 \sin{⁡a}+\sin{a}}{-\sin⁡ {a}}=\frac{4\sin{a}}{-\sin{a}}\)


 


Сократив на \(\sin⁡{a}\), получаем ответ.


\(=\frac{4 }{-1}=\)\(-4\)


 


Ответ:  \(-4\)


Пример. Вычислить чему равен \(ctg(-a-\frac{7π}{2})\), если \(tg\) \(⁡a=2\)


Решение:







\(ctg(-a-\frac{7π}{2}) =\)


Здесь сразу формулу приведения применять нельзя, так как аргумент нестандартный. Что не так? Прежде всего, \(a\) стоит первой, хотя должна быть после «точки привязки». Поменяем местами слагаемые аргумента, сохраняя знаки.


\(= ctg(-\frac{7π}{2}-a) =\)


 


Уже лучше, но все еще есть проблемы – «точка привязки» с минусом, а такого аргумента у нас нет. Избавимся от минуса, вынеся его за скобку внутри аргумента.



\(= ctg(-(\frac{7π}{2}+a)) =\)


 


Теперь вспомним о том, что котангенс – функция нечетная, то есть

\(ctg\) \((-t)=- ctg\) \(t\). Преобразовываем наше выражение.


\(= — ctg(\frac{7π}{2}+a) =\)


 


Несмотря на то, что точка привязки \(\frac{7π}{2}\) мы все равно можем использовать формулы приведения, потому что \(\frac{7π}{2}\) лежит на пересечении одной из осей и числовой окружности (смотри пояснение ниже). \((\frac{7π}{2}+a)\) это четвертая четверть, и котангенс там отрицателен. «Точка привязки» — вертикальная, то есть функцию меняем. Окончательно имеем \(ctg(\frac{7π}{2}+a)=-tg a\) .


\(= — (- tg\) \(a) = tg\) \(a = 2\)


 


Готов ответ.


Ответ:  \(2\)


Еще раз проговорим этот важный момент: с точки зрения формулы приведения \(\frac{7π}{2}\) — это тоже самое, что и \(\frac{3π}{2}\). Почему? Потому что \(\frac{7π}{2}=\frac{3π+4π}{2}=\frac{3π}{2}+\frac{4π}{2}=\frac{3π}{2}+2π\). Иными словами, они отличаются ровно на один оборот \(2π\). А на значения тригонометрических функций количество оборотов никак не влияет:


\(cos\) \(⁡t=cos ⁡(t+2π)=cos ⁡(t+4π)=cos ⁡(t+6π)= …=cos⁡ (t-2π)=cos ⁡(t-4π)=cos⁡ (t-6π)…\)

\(sin\) \(t=sin⁡ (t+2π)=sin ⁡(t+4π)=sin ⁡(t+6π)= . ..=sin⁡ (t-2π)=sin ⁡(t-4π)=sin ⁡(t-6π)…\)


Аналогично с тангенсом и котангенсом (только у них «оборот» равен \(π\)).

\(tg\) \(t=tg⁡(t+π)=tg⁡(t+2π)=tg⁡(t+3π)= …=tg⁡(t-π)=tg⁡(t-2π)=tg⁡(t-3π)…\)

\(ctg\) \(t=ctg⁡(t+π)=ctg⁡(t+2π)=ctg⁡(t+3π)= …=ctg⁡(t-π)=ctg⁡(t-2π)=ctg⁡(t-3π)…\)


Таким образом, \(-ctg(\frac{7π}{2}+a)=- ctg(\frac{3π}{2}+2π+a)=- ctg(\frac{3π}{2}+a)\).


То есть, для определения знака и необходимости смены функции важно лишь местоположение «точки привязки», а не её значение, поэтому так расписывать не обязательно (но можно если вы хотите впечатлить своими знаниями учительницу).

Ответы на часто задаваемые вопросы


Вопрос: Есть ли формулы приведения с аргументами \((\frac{π}{3}-a)\),\((\frac{π}{4}+a)\),\((\frac{7π}{6}+a)\) или тому подобное?
Ответ: К сожалению, нет. В таких ситуациях выгодно использовать формулы разности и суммы аргументов. Например, \(cos⁡(\frac{π}{3}-a)=cos⁡\frac{π}{3} cos⁡a+sin⁡\frac{π}{3} sin⁡a=\frac{1}{2}cos⁡a+\frac{\sqrt{3}}{2} sin⁡a\).


Смотрите также Как доказать тригонометрическое тождество?

18.3 Электрическое поле — физика

Раздел Цели обучения

К концу этого раздела вы сможете делать следующее:

  • Вычислять напряженность электрического поля
  • Создание и интерпретация рисунков электрических полей

Поддержка учителей

Поддержка учителей

Цели обучения в этом разделе помогут вашим учащимся освоить следующие стандарты:

  • (5) Учащийся знает природу сил в физическом мире. Ожидается, что студент:
    • (С)
      описать и рассчитать, как величина электрической силы между двумя объектами зависит от их зарядов и расстояния между ними.

Основные термины раздела

электрическое поле испытательный заряд

Поддержка учителей

Поддержка учителей

Спросите учащихся, видели ли они фильмы, в которых используется концепция полей как силовых полей . Попросите их описать, как работают такие поля. Опишите, как можно рассматривать гравитацию как поле, которое окружает массу и с которым взаимодействуют другие массы. Объясните, что электрические поля очень похожи на гравитационные поля.

Возможно, вы слышали о силовом поле в научно-фантастических фильмах, где такие поля применяют силы в определенных точках в космосе, чтобы удержать злодея в ловушке или защитить космический корабль от вражеского огня. Концепция поля очень полезна в физике, хотя она несколько отличается от того, что вы видите в кино.

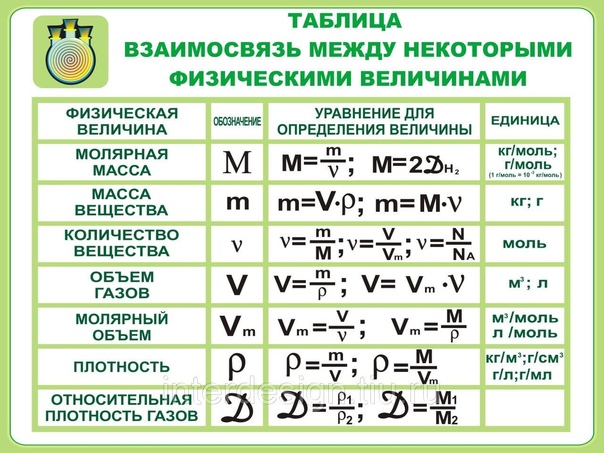
Поле — это способ концептуализации и отображения силы, которая окружает любой объект и действует на другой объект на расстоянии без видимой физической связи. Например, гравитационное поле, окружающее Землю и все другие массы, представляет гравитационную силу, которая возникла бы, если бы в данной точке поля была помещена другая масса.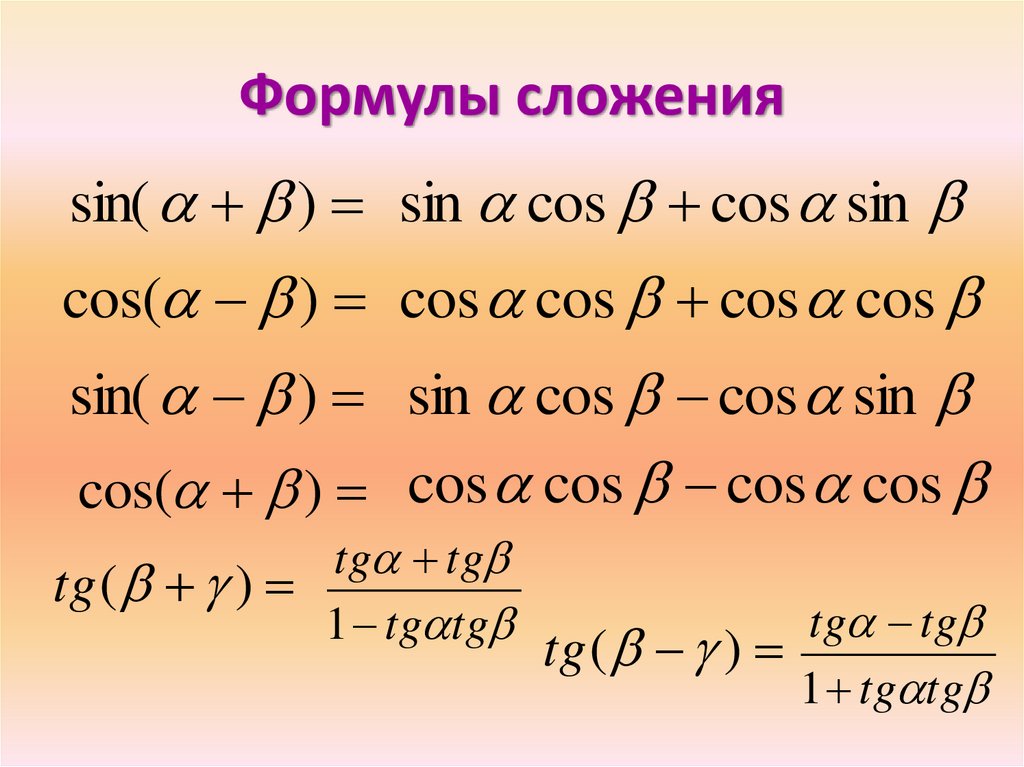 Майкл Фарадей, английский физик девятнадцатого века, предложил концепцию электрического поля. Если вы знаете электрическое поле, то можете легко рассчитать силу (величину и направление), действующую на любой электрический заряд, который вы поместите в поле.

Электрическое поле создается электрическим зарядом и сообщает нам силу на единицу заряда во всех местах в пространстве вокруг распределения заряда. Распределение заряда может быть одноточечным; распределение заряда, скажем, по плоской пластине; или более сложное распределение заряда. Электрическое поле распространяется в пространстве вокруг распределения заряда. Теперь рассмотрите возможность размещения пробного заряда в поле. Пробный заряд — это положительный электрический заряд, заряд которого настолько мал, что не возмущает существенно заряды, создающие электрическое поле. Электрическое поле действует на пробный заряд в заданном направлении. Приложенная сила пропорциональна заряду пробного заряда. Например, если мы удвоим заряд пробного заряда, сила, действующая на него, удвоится. Математически говоря, что электрическое поле представляет собой силу на единицу заряда, записывается как

E→=F→qtestE→=F→qtest

18.15

где мы рассматриваем только электрические силы. Обратите внимание, что электрическое поле представляет собой векторное поле, направленное в том же направлении, что и сила, действующая на положительный пробный заряд. Единицы электрического поля N/C.

Если электрическое поле создается точечным зарядом или сферой с однородным зарядом, то величина силы между этим точечным зарядом Q и пробным зарядом определяется законом Кулона

F=k|Qqtest|r2F =k|Qqtest|r2

, где используется абсолютное значение, потому что мы учитываем только величину силы. Тогда величина электрического поля равна

E=Fqtest=k|Q|r2.E=Fqtest=k|Q|r2.

18,16

Это уравнение дает величину электрического поля, создаваемого точечным зарядом Q . Расстояние r в знаменателе — это расстояние от точечного заряда Q или от центра сферического заряда до интересующей точки.

Если тестовый заряд удалить из электрического поля, электрическое поле все еще существует. Чтобы создать трехмерную карту электрического поля, представьте себе размещение пробного заряда в разных местах поля. В каждом месте измерьте силу, действующую на заряд, и используйте векторное уравнение E→=F→/qtestE→=F→/qtest для расчета электрического поля. Нарисуйте стрелку в каждой точке, где вы поместите пробный заряд, чтобы представить силу и направление электрического поля. Длина стрелок должна быть пропорциональна напряженности электрического поля. Если вы соедините эти стрелки вместе, вы получите линии. На рис. 18.17 показано изображение трехмерного электрического поля, создаваемого положительным зарядом.

Рисунок
18.17

Трехмерное представление электрического поля, создаваемого положительным зарядом.

Поддержка учителей

Поддержка учителей

[BL][OL]Укажите, что все силовые линии электрического поля берут начало от заряда.

[AL]Обратите внимание, что количество линий, пересекающих воображаемую сферу, окружающую заряд, одинаково независимо от размера сферы, которую вы выберете. Спросите, могут ли учащиеся использовать это, чтобы показать, что количество силовых линий, пересекающих поверхность на единицу площади, показывает, что напряженность электрического поля уменьшается пропорционально обратному квадрату расстояния.

Простое рисование линий электрического поля в плоскости, пересекающей заряд, дает двумерные карты электрического поля, показанные на рис. 18.18. Слева — электрическое поле, создаваемое положительным зарядом, а справа — электрическое поле, создаваемое отрицательным зарядом.

Обратите внимание, что силовые линии электрического поля направлены от положительного заряда к отрицательному. Таким образом, положительный пробный заряд, помещенный в электрическое поле положительного заряда, будет отталкиваться. Это согласуется с законом Кулона, согласно которому одноименные заряды отталкиваются друг от друга. Если мы поместим положительный заряд в электрическое поле отрицательного заряда, положительный заряд притянется к отрицательному заряду. Противоположное верно для отрицательных тестовых зарядов. Таким образом, направление линий электрического поля согласуется с тем, что мы находим, используя закон Кулона.

Уравнение E=k|Q|/r2E=k|Q|/r2 говорит о том, что электрическое поле становится сильнее по мере приближения к заряду, который его генерирует. Например, на расстоянии 2 см от заряда Q ( r = 2 см) электрическое поле в четыре раза сильнее, чем на расстоянии 4 см от заряда ( r = 4 см). Снова взглянув на рис. 18.17 и рис. 18.18, мы видим, что линии электрического поля становятся более плотными по мере приближения к заряду, который их генерирует. На самом деле плотность линий электрического поля пропорциональна напряженности электрического поля!

Рисунок
18.18

Линии электрического поля от двух точечных зарядов. Красная точка слева несет заряд +1 нКл, а синяя точка справа несет заряд -1 нКл. Стрелки указывают направление, в котором будет двигаться положительный пробный заряд. Линии поля сгущаются по мере приближения к точечному заряду.

Карты электрического поля могут быть составлены для нескольких зарядов или для более сложных распределений зарядов. Электрическое поле от нескольких зарядов можно найти, сложив электрические поля от каждого отдельного заряда. Поскольку эта сумма может быть только одним числом, мы знаем, что только одна линия электрического поля может проходить через любую заданную точку. Другими словами, линии электрического поля не могут пересекаться друг с другом.

На рис. 18.19(а) показана двумерная карта электрического поля, создаваемого зарядом + q и соседним зарядом — q . Трехмерная версия этой карты получается путем вращения этой карты вокруг оси, проходящей через оба заряда. Положительный пробный заряд, помещенный в это поле, будет испытывать силу в направлении силовых линий в его местоположении. Таким образом, он будет отталкиваться от положительного заряда и притягиваться к отрицательному заряду. Рисунок 18.19(b) показывает электрическое поле, создаваемое двумя зарядами − q . Обратите внимание, как силовые линии отталкиваются друг от друга и не перекрываются. Положительный пробный заряд, помещенный в это поле, будет притягиваться к обоим зарядам. Если вы находитесь далеко от этих двух зарядов, где далеко означает намного дальше, чем расстояние между зарядами, электрическое поле выглядит как электрическое поле от одного заряда -2 q .

Рисунок
18.19

(а) Электрическое поле, создаваемое точечным положительным зарядом (слева) и точечным отрицательным зарядом той же величины (справа). (б) Электрическое поле, создаваемое двумя равными отрицательными зарядами.

Поддержка учителей

Поддержка учителей

Попросите учащихся интерпретировать карты электрического поля. Где поле сильнее? Где поле слабее? В каком направлении поле увеличивается или уменьшается? Где поле наиболее однородно? Могут ли они проверить, что величина заряда одинакова в данной панели? Чем отличается поле двух отрицательных зарядов от поля положительного и отрицательного зарядов?

Виртуальная физика

Исследование электрического поля

Эта симуляция показывает вам электрическое поле из-за зарядов, которые вы размещаете на экране. Начните с установки верхнего флажка на панели параметров с правой стороны, чтобы отобразить электрическое поле. Перетащите заряды из ведер на экран, перемещайте их и наблюдайте за электрическим полем, которое они образуют. Чтобы более точно увидеть величину и направление электрического поля, перетащите датчик электрического поля или датчик электрического поля из нижнего ведра и перемещайте его по экрану.

Исследования PhET: заряды и поля.
Перемещайте точечные заряды по игровому полю, а затем просматривайте электрическое поле, напряжения, эквипотенциальные линии и многое другое.

Нажмите, чтобы просмотреть содержимое

Два положительных заряда размещены на экране. Какое утверждение описывает электрическое поле, создаваемое зарядами?

  1. Постоянно везде.

  2. Рядом с каждым зарядом ноль.

  3. Между зарядками ноль.

  4. Наибольшая сила на полпути между зарядами.

Смотреть физику

Электростатика (часть 2): интерпретация электрического поля

В этом видеоролике объясняется, как рассчитать электрическое поле точечного заряда и как интерпретировать карты электрического поля в целом. Обратите внимание, что лектор использует d для расстояния между частицами вместо r . Обратите внимание, что точечные заряды бесконечно малы, поэтому все их заряды сосредоточены в одной точке. Когда рассматриваются более крупные заряженные объекты, расстояние между объектами должно измеряться между центрами объектов.

Проверка захвата

Верно или неверно — если точечный заряд имеет силовые линии электрического поля, которые указывают на него, заряд должен быть положительным.

  1. правда
  2. ложно

Рабочий пример

Какова плата?

Посмотрите на рисунок электрического поля на рис. 18.20. Какова относительная сила и знак трех зарядов?

Рисунок
18.20

Карта электрического поля трех заряженных частиц.

Стратегия

Мы знаем, что электрическое поле простирается от положительного заряда и заканчивается отрицательным зарядом. Мы также знаем, что количество силовых линий электрического поля, которые касаются заряда, пропорционально заряду. Заряд 1 имеет 12 полей, выходящих из него. В заряд 2 входит шесть силовых линий. В заряд 3 входит 12 силовых линий.

Решение

Линии электрического поля выходят из заряда 1, так что это положительный заряд. Линии электрического поля проходят через заряды 2 и 3, поэтому они являются отрицательными зарядами. Отношение зарядов равно q1:q2:q3=+12:-6:-12q1:q2:q3=+12:-6:-12. Таким образом, величина зарядов 1 и 3 вдвое превышает величину заряда 2.

Обсуждение

Хотя мы не можем определить точный заряд каждой частицы, мы можем получить много информации из электрического поля относительно величины и знака зарядов. и где сила пробного заряда будет наибольшей (или наименьшей).

Рабочий пример

Электрическое поле от дверной ручки

Дверная ручка, которую можно принять за сферический металлический проводник, приобретает заряд статического электричества q=-1,5 нКл. q=-1,5 нКл. Чему равно электрическое поле на расстоянии 1,0 см от дверной ручки? Диаметр дверной ручки 5,0 см.

Стратегия

Поскольку дверная ручка является проводником, весь заряд распределяется по внешней поверхности металла. Кроме того, поскольку дверная ручка считается идеально сферической, заряд на поверхности распределяется равномерно, поэтому мы можем рассматривать дверную ручку так, как если бы весь заряд был сосредоточен в центре дверной ручки. Справедливость этого упрощения будет доказана в следующем курсе физики. Теперь нарисуйте дверную ручку и определите вашу систему координат. Используйте +x+x, чтобы указать внешнее направление, перпендикулярное двери, с x=0x=0 в центре дверной ручки (как показано на рисунке ниже).

Если диаметр дверной ручки 5,0 см, ее радиус 2,5 см. Мы хотим знать электрическое поле на расстоянии 1,0 см от поверхности дверной ручки, что составляет расстояние r = 2,5 см + 1,0 см = 3,5 см, r = 2,5 см + 1,0 см = 3,5 см от центра дверной ручки. Мы можем использовать уравнение E=k|Q|r2E=k|Q|r2, чтобы найти величину электрического поля. Направление электрического поля определяется знаком заряда, который в данном случае отрицательный.

Решение

Введение заряда Q=-1,5 нКл=-1,5×10-9.

Обсуждение

Похоже на огромное электрическое поле. К счастью, требуется электрическое поле примерно в 100 раз сильнее (3×106 Н/Кл3×106 Н/Кл), чтобы заставить воздух разлагаться и проводить электричество. Кроме того, вес взрослого человека составляет около 70 кг × 9,8 м/с2 ≈ 700 Н70 кг × 9,8 м/с2 ≈ 700 Н, так почему вы не чувствуете силы, действующей на протоны в вашей руке, когда вы тянетесь к дверной ручке? Причина в том, что ваша рука содержит равное количество отрицательного заряда, который отталкивает отрицательный заряд дверной ручки. Из-за поляризации в вашей руке может развиться очень небольшая сила, но вы никогда этого не заметите.

Практические задачи

15.

Какова величина электрического поля на расстоянии 20 см от точечного заряда q = 33 нКл?

  1. 7,4 × 10 3 Н/З
  2. 1,48 × 10 3 Н/З
  3. 7,4 × 10 12 Н/З
  4. 0

16.

Заряд -10 нКл находится в начале. В каком направлении электрическое поле от заряда указывает на х + 10 см?

  1. Электрическое поле направлено в сторону от отрицательных зарядов.
  2. Электрическое поле указывает на отрицательные заряды.
  3. Электрическое поле направлено в сторону положительных зарядов.
  4. Электрическое поле направлено в сторону от положительных зарядов.

Проверьте свое понимание

17.

Когда силовые линии электрического поля сближаются, что это говорит вам об электрическом поле?

  1. Электрическое поле обратно пропорционально плотности линий электрического поля.
  2. Электрическое поле прямо пропорционально плотности линий электрического поля.
  3. Электрическое поле не связано с плотностью линий электрического поля.
  4. Электрическое поле обратно пропорционально квадратному корню из плотности силовых линий электрического поля.

18.

Если пять линий электрического поля исходят из заряда +5 нКл, сколько линий электрического поля должно исходить из заряда +20 нКл?

  1. пять линий поля
  2. 10 строк поля
  3. 15 строк поля
  4. 20 строк поля

Электрическое поле, сферическая геометрия

Электрическое поле, сферическая геометрия

Электрическое поле точечного заряда Q можно получить прямым применением закона Гаусса. Рассматривая гауссову поверхность в виде сферы радиусом r , электрическое поле имеет одинаковую величину в каждой точке сферы и направлено наружу. Тогда электрический поток равен произведению электрического поля на площадь сферы.

Электрическое поле на радиусе r определяется как:

Если другой заряд q поместить в r , он будет
испытать силу

, так что это считается согласующимся с законом Кулона.

Заряженная проводящая сфера Сфера однородного заряда

Поля для другой геометрии заряда

 Индекс

Концепции электрического поля

 

Гиперфизика***** Электричество и магнетизм R Ступица
Назад

Электрическое поле проводящего шара с зарядом Q можно получить прямым применением закона Гаусса. Рассматривая гауссову поверхность в виде сферы радиусом r > R , электрическое поле имеет одинаковую величину в каждой точке поверхности и направлено наружу. Тогда электрический поток равен произведению электрического поля на площадь сферической поверхности.

Видно, что электрическое поле идентично полю точечного заряда Q в центре сферы. Поскольку весь заряд будет находиться на проводящей поверхности, поверхность Гаусса при r

Point charge Sphere of uniform charge

Potential of conducting sphere

Fields for other charge geometries

 Индекс

Концепции электрического поля

 

Гиперфизика***** Электричество и магнетизм R Ступица
Назад

Электрическое поле сферы с однородной плотностью заряда и полным зарядом заряда Q можно получить, применяя закон Гаусса. Рассматривая гауссову поверхность в виде сферы с радиусом r > R , электрическое поле имеет одинаковую величину в каждой точке поверхности и направлено наружу. Тогда электрический поток равен произведению электрического поля на площадь сферической поверхности.

Видно, что электрическое поле вне сферы ( r > R ) идентично полю точечного заряда Q в центре сферы.
Для радиуса r гауссова поверхность будет охватывать меньше, чем полный заряд, и электрическое поле будет меньше. Внутри сферы заряда поле определяется как:

Точечный заряд Заряженная проводящая сфера

Поля для другой геометрии заряда

 Индекс

Концепции электрического поля

 

Гиперфизика***** Электричество и магнетизм R Ступица
Назад

Электрическое поле внутри сферы с однородным зарядом направлено радиально наружу (по симметрии), но сферическая гауссова поверхность заключала бы в себе меньше полного заряда Q.

Читайте также: