Формулы хл: 15 формул в Excel, которые помогут в работе

Правильное округление данных Excel для получения правильных сумм

При компиляции данных для отчета или презентации PowerPoint округление сумм в Excel часто вызывает проблемы. Во многих случаях требуется, чтобы округленные итоговые значения совпадали с итоговыми значениями округленных слагаемых, но этого сложно достичь. Для примера рассмотрим следующую таблицу:

Если значения округляются до целых чисел с помощью функции форматирования ячеек Excel, результатом будет следующая таблица. Итоговые значения, вычисленные «неправильно», выделены полужирным шрифтом:

Аналогично при использовании стандартных функций округления итоговые значения округленных значений вычисляются правильно, однако ошибки округления накапливаются, из-за чего результаты часто существенно отличаются от фактических сумм исходных значений. В следующей таблице показан результат =ROUND(x,0) примера выше. Суммы, которые отличаются от исходного значения на 1 и более, выделены полужирным шрифтом:

Используя округление think-cell, можно получить согласованные округленные суммы с минимальными изменениями. Хотя большинство значений округляются до ближайшего целого числа, некоторые значения округляются в противоположном направлении, что гарантирует правильное вычисления без накопления ошибки округления. Так как существует много способов получения правильных округленных сумм за счет изменения значений, think-cell выбирает решение, для которого требуется изменить минимальное число значений и минимальное отклонение от точных значений. Например, округление 10,5 до 10 будет предпочтительнее, чем округление 3,7 до 3. В следующей таблице показано оптимальное решение для примера выше, при этом измененные значения выделены полужирным шрифтом:

Чтобы получить такой же результат в собственных вычислениях, просто выберите соответствующий диапазон ячеек Excel. Затем нажмите кнопку на вкладке Формулы и, при необходимости, измените точность округления, используя раскрывающийся список на панели инструментов.

22.1
Использование округления think-cell
22. 2
Ограничения округления think-cell
22.3
Устранение неполадок с формулами TCROUND

22.1 Использование округления think-cell

Округление think-cell полностью интегрируется с Microsoft Excel и предоставляет набор функций, которые похожи на стандартные функции округления Excel. Вы легко можете применять эти функции к собственным данным, используя кнопки на панели инструментов на вкладке Формулы в think-cell.

22.1.1 Параметры округления

Как и функции Excel, функции округления think-cell принимают два параметра.

x
Значение, которое необходимо округлить. Это может быть константа, формула или ссылка на другую ячейку.
n
Точность округления. Значение этого параметра зависит от используемой функции. Параметры функций think-cell эквивалентны параметрам соответствующих функций Excel. Примеры см. в таблице ниже.

Округление think-cell позволяет округлять значения не только до целых чисел, но и до любых кратных чисел. Например, если вы хотите представить данные в последовательности 5-10-15…, просто округляйте значения до чисел, кратных пяти. Используя раскрывающееся меню на панели инструментов think-cell, просто введите или выберите нужную точность округления. Затем think-cell выберет требуемые функцию и параметры. В следующей таблице представлен ряд примеров округления определенных значений x с использованием панели инструментов вместе с соответствующим параметром n.

x =

n =

10050210,01
1,01800211,02
1700181717,00
54,610050555454,60
1234,123412001250123412341234,12
8776,5432188008800877687778776. 54

Если значения отображаются не так, как вы ожидаете, убедитесь, что в параметрах формата ячейки Excel выбрано значение Общий, а столбцы достаточно широкие для отображения всех знаков после запятой.

КнопкаФормулаОписание
TCROUND(x, n) Позволить think-cell определять ближайшее кратное число для округления, чтобы минимизировать ошибку округления.
TCROUNDUP(x, n) Принудительное округление x от нуля.
TCROUNDDOWN(x, n) Принудительное округление x к нулю.
TCROUNDNEAR(x, n) Принудительное округление x к ближайшему кратному числу с требуемой точностью.
Удалить все функции округления think-cell из выбранных ячеек.
Выберите или введите требуемое кратное число для округления.
Выделить все ячейки, которые надстройка think-cell решила округлить до наиболее отдаленного из двух кратных чисел вместо наиболее близкого числа.
Вращающееся колесико означает, что функция округления think-cell применяется.

Для получения оптимальных результатов и минимального отклонения от базовых значений, следует использовать TCROUND, когда это возможно. Используйте более ограничительные функции TCROUNDDOWN, TCROUNDUP или TCROUNDNEAR, только если это необходимо.

Внимание! Не следует использовать недетерминированные функции, такие как RAND(), с какими-либо формулами TCROUND. Если функции возвращают разные значения при каждом вычислении, округление think-cell будет совершать ошибки при вычислении значений.

22.1.2 Макет вычисления

Прямоугольный макет примера выше приведен исключительно для демонстрации.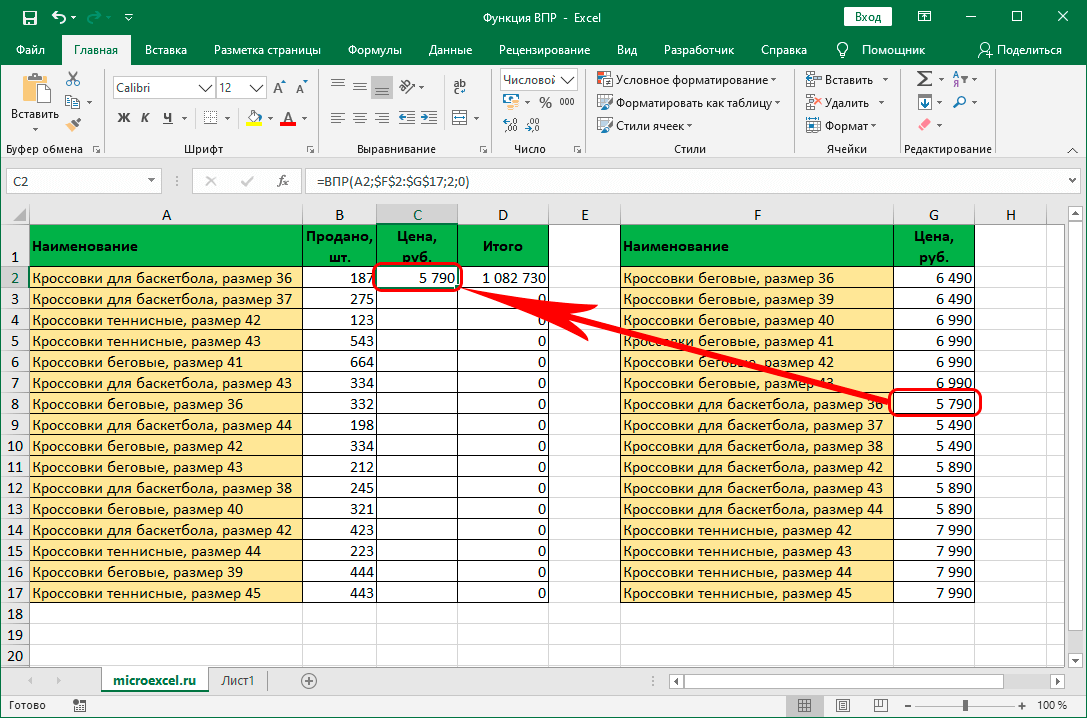 Вы можете использовать функции TCROUND, чтобы настроить отображение произвольных сумм на листе Excel. Трехмерные ссылки Excel на другие листы и ссылки на другие файлы также работают.

22.1.3 Размещение функций TCROUND

Так как функции TCROUND предназначены для управления выходными данными ячейки, они должны быть крайними функциями:

Неправильно: =TCROUND(A1, 1)+TCROUND( SUM(B1:E1), 1 )
Правильно:=TCROUND( A1+SUM(B1:E1), 1 )
 
Неправильно:=3*TCROUNDDOWN(A1, 1)
Правильно: =TCROUNDDOWN(3*A1, 1)

Если вы введете что-то в строках неправильных примеров, think-cell уведомит вас о значении ошибки Excel #VALUE!.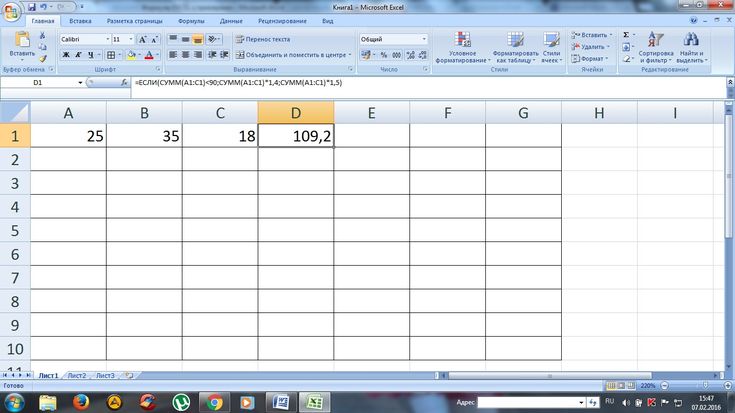

22.2 Ограничения округления think-cell

Округление think-cell всегда ищет решение для произвольных сумм с промежуточными итогами и итоговыми значениями. Округление think-cell также предоставляет подходящие решения для других вычислений, использующих умножение и числовые функции. Однако в математических целях существование согласованного округляемого решения не может гарантироваться, если используются операторы, отличные от +, — и SUM.

22.2.1 Умножение на константу

Во многих случаях округление think-cell дает хорошие результаты, если используется умножение на константу, то есть если хотя бы один из коэффициентов основан на результате другой функции TCROUND. Рассмотрим следующий пример:

Точный результат вычисления для ячейки C1: 3×1,3+1,4=5,3. Чтобы получить этот результат, можно округлить значение 1,4 до 2:

Однако округление think-cell может только изменить значение, округлив его до большего или меньшего значения. Большее отклонение от исходных значений не поддерживается. Поэтому для определенных сочетаний входных значений невозможно найти согласованное решение для округления. В этом случае функция TCROUND предоставляет значение ошибки Excel #NUM!. В следующем примере показана нерешаемая задача:

Точный результат вычисления для ячейки C1: 6×1,3+1,4=9,2. Округление ячеек A1 и B1 даст следующий результат: 6×1+2=8 или 6×2+1=13. Фактический результат нельзя округлить до 8 или 13, а выходные данные округления think-cell будут выглядеть следующим образом:

Примечание. Функция AVERAGE Excel интерпретируется округлением think-cell как комбинация суммирования и умножения на константу. Кроме того, сумма, в которой одно слагаемое используется несколько раз, математически эквивалентно умножению на константу, и существование решения не гарантируется.

22.2.2 Общее умножение и другие функции

Если функции TCROUND используются для соответствующих ячеек и промежуточные результаты связаны только операторами +, -, SUM и AVERAGE, слагаемые и (промежуточные) итоговые значения объединяются в одной задаче округления. В этих случаях округление think-cell найдет решение, которое обеспечивает согласованность для всех связанных ячеек, если такое решение существует.

Так как TCROUND — обычная функция Excel, ее можно объединить с любыми функциями и операторами. Но если вы используете функции, отличные от указанных выше, для соединения результатов операторов TCROUND, округление think-cell не может объединить компоненты в одной общей задаче. Вместо этого компоненты формулы будут считаться отдельными задачами, каждая из которых будет решаться независимо друг от друга. Затем результаты будут использоваться как входные данные для других формул.

Во многих случаях результаты округления think-cell по-прежнему будут рациональными. Однако в некоторых случаях использование операторов, отличных от +, -, SUM и AVERAGE, приводит к получению округленных результатов, которые существенно отличаются от вычисления без округления. Рассмотрим следующий пример:

Точный результат вычисления для ячейки C1 в этом случае: 8,6×1,7=14,62.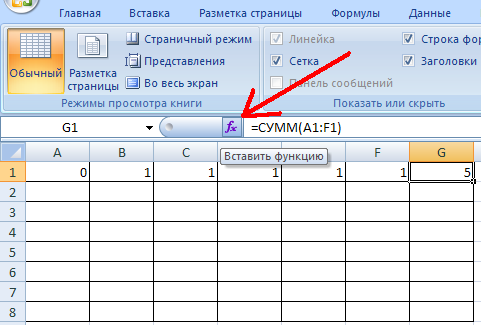 Так как ячейки A1 и B1 связаны умножением, округление think-cell не сможет объединить формулы из этих ячеек в общую задачу. Вместо этого после обнаружения ячейки A1 как допустимых входных данных, ячейка B1 будет вычислена независимо, а результат будет считаться константой для оставшейся задачи. Так как других ограничений нет, значение 1,7 из ячейки B1 округляется до ближайшего целого числа (2).

«Точный» результат вычисления для ячейки C1 в этом случае: 8,6×2=17,2. Теперь эту задачу попытается решить функция округления think-cell. Существует согласованное решение, для которого необходимо округлить 17,2 до 18. Результат будет выглядеть следующим образом:

Обратите внимание, что округленное значение в ячейке C1, которое равно 18, сильно отличается от исходного значения 14,62.

22.3 Устранение неполадок с формулами TCROUND

При использовании округления think-cell вы можете столкнуться с двумя ошибками: #VALUE! и #NUM!.

22.3.1 #VALUE!

Ошибка #VALUE! указывает на синтаксические проблемы, такие как неправильно введенные формулы или недопустимые параметры.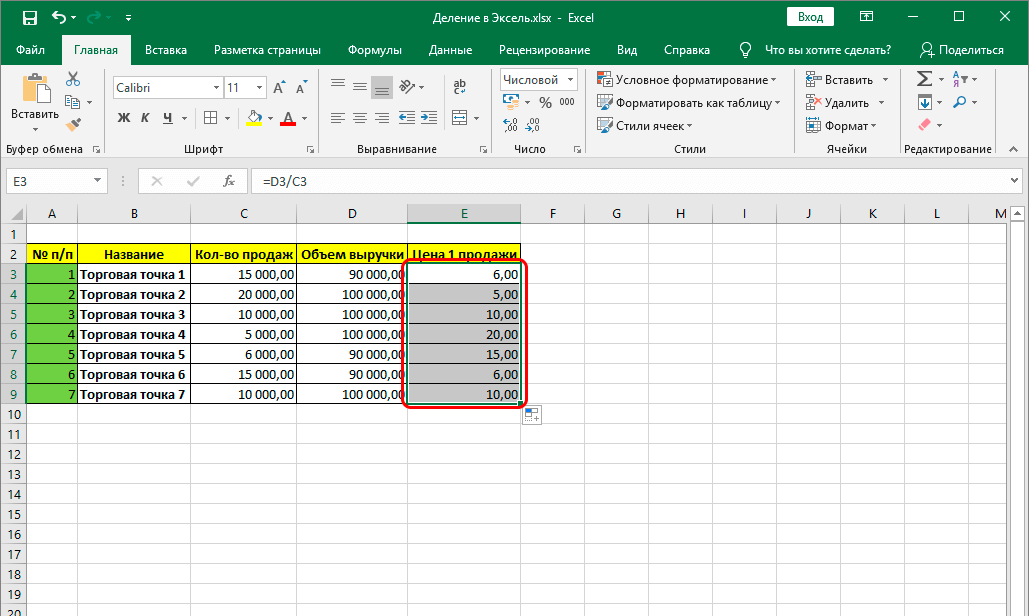 Например, второй параметр TCROUND должен быть целым числом. Кроме того, уделите внимание правильному использованию разделителей. Например, в международной версии Excel формула выглядит так: =TCROUND(1.7, 0), а в немецкой версии Excel ее следует записать следующим образом: =TCROUND(1,7; 0).

Еще одна ошибка, связанная с округлением think-cell, — это размещение вызова функции TCROUND: нельзя использовать функцию TCROUND с другой формулой. Убедитесь, что TCROUND — это крайняя функция в формуле ячейки. (См. раздел Размещение функций TCROUND.)

22.3.2 #NUM!

Ошибка #NUM! возникает из-за числовых проблем. Если результат функции TCROUND равен #NUM!, это значит, что задача, определенная данным набором формул, не имеет математического решения. (См. раздел Ограничения округления think-cell.)

Если формулы, окруженные функциями TCROUND, содержат только операторы +, — и SUM и для всех операторов TCROUND используется одинаковая точность (второй параметр), решение будет гарантированно существовать и будет найдено округлением think-cell. Однако в следующих случаях существование согласованного округленного решения не гарантируется.

  • Формулы содержат другие операции, такие как умножение или числовые функции. Кроме того, суммы, в которых одно слагаемое используется несколько раз, математически эквивалентны умножению.
  • Вы должны использовать разные точности во втором параметре функции TCROUND.
  • Вы часто используете функции TCROUNDDOWN, TCROUNDUP и TCROUNDNEAR.

Вы можете заново сформулировать задачу, чтобы получить согласованное решение. Попробуйте следующее:

  • Используйте более высокую точность для некоторых или всех операторов TCROUND.
  • Не используйте TCROUND с умножением или числовыми функциями, отличными от +, — и SUM.
  • Используйте одинаковую точность (второй параметр) для всех операторов TCROUND.
  • Используйте TCROUND вместо функций TCROUNDDOWN, TCROUNDUP и TCROUNDNEAR, где это возможно.

Excel Редактор онлайн бесплатно


редактор

Зритель

Преобразование

Слияние

Разблокировать

Защищать

Сплиттер

Сравнение

Аннотация

Парсер

Метаданные

Водяной знак

Поиск

Заменять

Повернуть

Обеспечить регресс

Диаграмма

Ипотека

Сборка

Перевод

Компресс

Прозрачный

ИМТ

ВебКонвертер


Питаться от

aspose. com

&

aspose.cloud



Перетащите или загрузите свои файлы


Введите адрес








*Загружая свои файлы или используя наш сервис, вы соглашаетесь с нашими

Условия использования

&

политика конфиденциальности











Создайте новый файл Excel из галереи шаблонов:


Расширять


Поделиться через фейсбук


Поделиться в Твиттере


Посмотреть другие приложения


Попробуйте наш облачный API


См. исходный код


Оставить отзыв


Добавить это приложение в закладки


Нажмите Ctrl + D, чтобы добавить эту страницу в избранное, или Esc, чтобы отменить действие.

Вы хотите сообщить об этой ошибке на форум, чтобы мы могли изучить ее и решить проблему? Вы получите уведомление по электронной почте, когда ошибка будет исправлена.


Email:


Сделайте этот форум закрытым, чтобы он был доступен только вам и нашим разработчикам.



Вы успешно сообщили об ошибке. Вы получите уведомление по электронной почте, когда ошибка будет исправлена.

Нажмите эту ссылку, чтобы посетить форумы.


Вы уверены, что хотите удалить файлы?


Обработка…

Формулы для определения хлорофилловых пигментов, экстрагированных N,N-диметилформамидом 1 | Физиология растений

Фильтр поиска панели навигации

Физиология растенийЭтот выпускЖурналыАмериканского общества биологов растенийНауки о растениях и лесоводствоКнигиЖурналыOxford Academic
Мобильный телефон Введите поисковый запрос

Закрыть

Фильтр поиска панели навигации

Физиология растенийЭтот выпускЖурналыАмериканского общества биологов растенийНауки о растениях и лесоводствоКнигиЖурналыOxford Academic
Введите поисковый запрос

Расширенный поиск

Журнальная статья

Рами Моран

Рами Моран

Ищите другие работы этого автора на:

Оксфордский академический

Google Scholar

Физиология растений , том 69, выпуск 6, июнь 1982 г. , страницы 1376–1381, https://doi.org/10.1104/pp.69.6.1376

Опубликовано:

01 июня 1983 г.

0030

  • PDF

  • Разделенный вид

    • Содержание статьи
    • Рисунки и таблицы
    • видео
    • Аудио
    • Дополнительные данные

  • Цитировать

    Процитируйте

    Рами Моран, Формулы для определения хлорофилловых пигментов, экстрагированных с помощью N,N -диметилформамида, Физиология растений , Том 69, Выпуск 6, 19 июня82, страницы 1376–1381, https://doi. org/10.1104/pp.69.6.1376

    Выберите формат
    Выберите format.ris (Mendeley, Papers, Zotero).enw (EndNote).bibtex (BibTex).txt (Medlars, RefWorks)

    Закрыть

  • Разрешения

    • Электронная почта
    • Твиттер
    • Фейсбук
    • Подробнее

    • Фильтр поиска панели навигации

    Физиология растенийЭтот выпускЖурналыАмериканского общества биологов растенийНауки о растениях и лесоводствоКнигиЖурналыOxford Academic
    Мобильный телефон Введите поисковый запрос

    Закрыть

    Фильтр поиска панели навигации

    Физиология растенийЭтот выпускЖурналыАмериканского общества биологов растенийНауки о растениях и лесоводствоКнигиЖурналыOxford Academic
    Введите поисковый запрос

    Расширенный поиск

    Экстракция хлорофиллов в тканях высших растений с использованием N,N -диметилформамида ускоряет процесс и позволяет определять небольшие образцы с низким уровнем пигмента.

    Были записаны спектры поглощения Chl a , Chl b и Pchl и их подкисленных производных, феофитинов. Превращение Chl b в соответствующий ему подкисленный продукт происходит гораздо медленнее, чем у Chl 9.0023 и и Пхл. В подкисленном состоянии Пхл отличается от Хл а и Хл б исчезновением красной полосы в спектре поглощения. Определены удельные коэффициенты экстинкции и разработаны формулы для количественного определения концентраций пигментов. При низких концентрациях пигментов, как в этиолированном растительном сырье, спектры поглощения хлорофиллов могут быть искажены из-за присутствия одновременно экстрагируемых других веществ; также были выведены формулы для определения пигмента в таких условиях.

    1

    Частично финансируется Фондом исследований ботаники, посвященным памяти Цви Мериамински и его сестры Сони Мериамински. Мы благодарим доноров за их вклад.

    Этот контент доступен только в формате PDF.

    © 1982 Американское общество биологов растений

    Эта статья публикуется и распространяется на условиях издательства Oxford University Press, Standard Journals Publication Model (https://academic.oup.com/journals/pages/open_access/funder_policies/chorus /стандартная_публикация_модель)

    Раздел выпуска:

    Статьи

    Скачать все слайды

    Реклама

    Цитаты

    Альтметрика

    Дополнительная информация о метриках

    Оповещения по электронной почте

    Оповещение об активности статьи

    Предварительные уведомления о статьях

    Оповещение о новой проблеме

    Оповещение о теме

    Получайте эксклюзивные предложения и обновления от Oxford Academic

    Ссылки на статьи по телефону

    • Последний

    • Самые читаемые

    • Самые цитируемые

    Крупные клетки коры корня и уменьшенные файлы клеток коры улучшают рост при неоптимальном азоте in silico

    Модулирование реакции ауксина стабилизирует завязывание плодов томатов

    Белки, подобные хлоропластному Sec14, модулируют рост и реакцию дефицита фосфатов у арабидопсиса и риса

    Расхождение транскриптома и метилома ДНК в развитии соцветия между двумя экотипами Panicum Hallii

    РЕГУЛИРУЕМЫЕ ХОЛОДОМ ГЕНЫ 27 и 28 противодействуют транскрипционной активности циркадианного комплекса RVE8/LNK1/LNK2

    Реклама

    NASA Ocean Color

    Содержание

    1. Краткое описание продукта
    2. Описание алгоритма
    3. Предыдущие версии
    4. Каталожные номера
    5. Доступ к данным

    1 — Обзор продукта

    Этот алгоритм возвращает приповерхностную концентрацию хлорофилла-а (хлор_а) в
    мг м -3 , рассчитанное с использованием эмпирических соотношений, полученных на основе измерений хлора in situ и отражательной способности дистанционного зондирования ($R_{rs}$).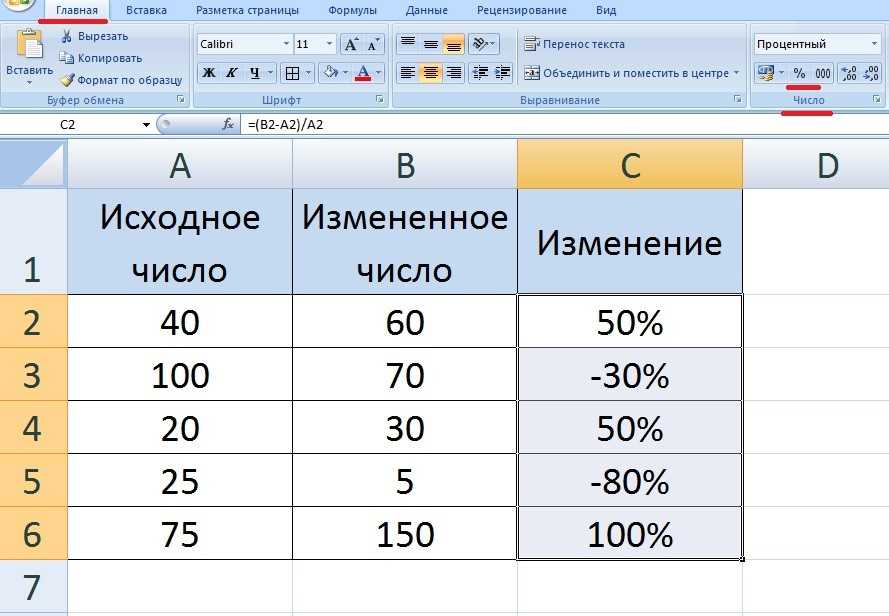 Реализация зависит от наличия трех или более диапазонов датчиков, охватывающих спектральный режим 440–670 нм. Алгоритм применим ко всем современным датчикам цвета океана. 9Продукт 0198 chlor_a входит в состав стандартного комплекта продуктов Level-2 OC и комплекта продуктов Level-3 CHL.

    Текущая реализация стандартного продукта хлорофилла (chlor_a), применяемая в версии R2022 многоцелевой обработки цвета океана НАСА, представляет собой смесь обновленного алгоритма отношения полос OC3/OC4 (OCx) (O’Reilly and Werdell 2019) и цветовой индекс (CI) Hu et al. (2019). Комбинированный алгоритм и теоретическая основа описаны в Hu et al. (2019), а текущая реализация подробно описана ниже.

    MODIS Aqua chlor_a сезонный композит на весну 2014 г.

    Алгоритм Контактное лицо: П. Джереми Верделл, Центр космических полетов имени Годдарда НАСА; Chuanmin Hu, Университет Южной Флориды

    2 — Описание алгоритма

    Входные данные:

    $R_{rs}$ на 2-4 длинах волн от 440 до 670 нм

    Выходы:

    хлор_а , концентрация хлорофилла а в мг·м -3

    Подход:

    Текущий стандартный продукт chlor_a основан на алгоритме Hu et al.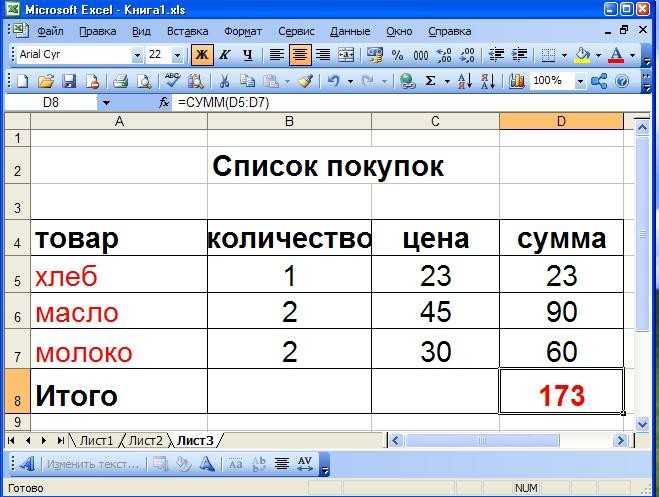 (2019), который сочетает в себе эмпирический подход разности полос при низких концентрациях хлорофилла с подходом соотношения полос при более высоких концентрациях хлорофилла. Подход, основанный на разности полос, — это цветовой индекс или CI (Hu et al. 2019), а подход соотношения полос основан на серии алгоритмов OCx, представленных в O’Reilley et al. 1998, с обновленными коэффициентами от O’Reilley и Werdell ( 2019).

    Алгоритм работает следующим образом:

    1. Концентрация хлорофилла сначала рассчитывается с использованием алгоритма CI, который представляет собой трехполосный алгоритм разности коэффициентов отражения, использующий разницу между специфическими для датчика Rrs в зеленой полосе и эталоном, формируемым линейно между Rrs в синие и красные полосы (полосы зависят от прибора — см. Таблицу 1):
      $$CI = R_{rs}(\lambda_{зеленый}) — [R_{rs}(\lambda_{синий}) + (\lambda_{зеленый }-\lambda_{синий)}/(\lambda_{красный}-\lambda_{синий}) * (R_{rs}(\lambda_{красный})-R_{rs}(\lambda_{синий}))]$ $
      9я$$

      где числитель, $R_{rs}(\lambda_{blue})$, является наибольшим из нескольких входных значений $R_{rs}$ и коэффициентов, a 0 — a 4 , зависят от датчика (таблица 1). В большинстве случаев они взяты непосредственно из O’Reilley and Werdell (2019).

      Таблица 1. Коэффициенты для серии алгоритмов OCx при стандартной обработке.
      датчик Алгоритм OCx R rs б/у
      (синий/зеленый)      		 и (0,1,2,3,4)
      SeaWiFS ОС4, ДИ руб.(443>489>510)/555 руб. 0,32814; -3,20725; 3.22969; -1,36769; -0,81739
      МОДИС ОС3М, КИ руб.(443>488)/547 руб. 0,26294; -2,64669; 1,28364; 1.08209; -1,76828
      ВИРС-СНЭС OC3_VIIRS_SNPP, КИ руб.(443>486)/551 руб. 0,23548; -2,63001; 1,65498; 0,16117; -1,37247
      VIIRS-NOAA20 OC3_VIIRS_NOAA20, КИ руб. (445>489)/556 руб. 0,28153; -2,65472; 1.30882; 1.31521; -2,08622
      VIIRS-NOAA21 OC3_VIIRS_NOAA21, КИ руб.(445>488)/555 руб. 0,24765; -2,54926; 1,55323; 0,39485; -1,54632
      МЕРИС OC4E, КИ руб.(443>489>510)/560 руб. 0,42487; -3,20974; 2,89721; -0,75258; -0,98259
      ОКТ ОС4О, КИ руб.(443>489>516)/565 руб. 0,54655; -3,51799; 3,39128; -0,91567; -0,97112
      ГОЧИ ОС4, КИ руб.(412>443>489)/555 руб. 0,28043; -2,49033; 1,53980; -0,09926; -0,68403
      ЯСТРОЙ ОС4, ДИ руб.(447>488>510)/556 руб. 0,32814, -3,20725, 3,22969, -1,36769, -0,81739
      ОЛКИ ОС4, ДИ руб. (443>490>510)/560 руб. 0,42540; -3,21679; 2,86907; -0,62628; -1,09333
      ЧСС ОС3, КИ руб.(443>520)/555 руб. 0,31841; -4,56386; 8,63979; -8.41411; 1.91532
    2. Для извлечения хлорофилла ниже 0,25 мг м -3 используется алгоритм CI.
      Для извлечения хлорофилла выше 0,35 мг м -3 используется алгоритм OCx.
      Между этими значениями алгоритмы CI и OCx смешиваются с использованием взвешенного подхода, где: }+\frac{хлор\_a_{OCx}(хлор\_a_{CI}-t_1)}{t_2-t_1}$$

      с t 1 = 0,25 и t 2 = 0,35 (края текущей области смешивания).

    Для алгоритма CI ближайший к 443, 555 и 670 нм диапазон используется для синего, зеленого и красного диапазонов соответственно для всех датчиков. Для датчиков, которые не имеют полосы, очень близкой к 555 нм, выполняется коррекция для смещения ближайшей зеленой полосы 9{(a_1*log_{10}(R_{rs}(\lambda_0))-b_1)}$$
    Если R rs (λ 0 ) ≥ sw,
    $$R_{rs}(555 )=a_2*R_{rs}(\lambda_0)-b_2$$
    Для различных спектральных полос (λ 0 ), sw и a 1 , b 1 , 9023 3 9 , и b 2 приведены в табл.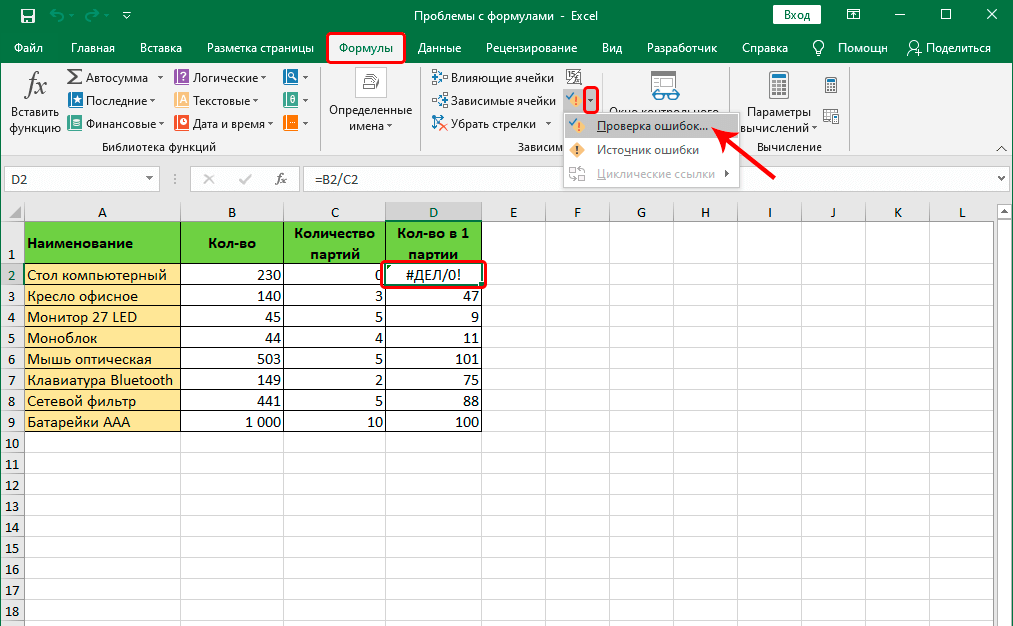 2.

    Таблица 2. Спектрально-полосные удельные коэффициенты sw, a 1 b 1 , а 2 и б 2 .
    Спектральный диапазон (λ 0 , нм) ПО а 1 , б 1 а 2 , б 2
    543 — 547 0,001723 0,986; 0,081495 1,031; 0,000216
    548 — 552 0,001597 0,988; 0,062195 1,014; 0,000128
    558 — 562 0,001148 1,023; -0,103624 0,979; -0,000121
    563 — 567 0,000891 1,039; -0,183044 0,971; -0,000170

    3 — Предыдущие версии

    Вкратце, оба продукта хлорофилла рассчитываются, а затем смешиваются с переходом между CI и OCx при 0,25-3. В некоторых случаях, когда O’Reilly и Werdell 2019 не предлагали обновления алгоритма соотношения полос OCx, коэффициенты оставались такими же, как и в предыдущих реализациях.
    В более старых реализациях использовались O’Reilly et al. (1998) подход к получению коэффициентов из версии 2 набора данных биооптического морского алгоритма НАСА (NOMAD), объединенного с CI, с использованием коэффициентов Hu et al (2012) с той же переходной зоной (0,15).

    4 — Ссылки

    Ху, К., Ли, З., и Франц, Б. (2012). Алгоритмы хлорофилла а для олиготрофных океанов: новый подход, основанный на трехполосной разнице коэффициентов отражения. Журнал геофизических исследований, 117 (C1). doi: 10.1029/2011jc007395

    Ху, К., Фэн, Л., Ли, З., Франц, Б.А., Бейли, С.В., Верделл, П.Дж., и Проктор, К.В. (2019). Улучшение продуктов спутниковых глобальных данных по хлорофиллу а посредством уточнения алгоритма и восстановления данных. Журнал геофизических исследований: Океаны, 124 (3), 1524–1543, doi: 10.

    Читайте также: