Формула а работы: Все формулы по физике за 7 класс с пояснениями — таблица и шпаргалки

Все формулы по физике за 7 класс с пояснениями — таблица и шпаргалки

Научим применять физические формулы для решения задач

Начать учиться

400.5K

Готовясь к экзаменам, удобно иметь под рукой шпаргалку, где будет кратко изложено самое важное. В этом материале мы объединили все основные формулы по физике за 7 класс с пояснениями и терминами. Их можно скачать на свой компьютер, чтобы всегда иметь под рукой.

Шпаргалки по физике за 7 класс

В рамках одной статьи сложно охватить весь курс по физике, но мы осветили основные темы за 7 класс и этого достаточно, чтобы освежить знания в памяти. Скачайте и распечатайте обе шпаргалки — одна из них (подробная) пригодится для вдумчивой подготовки к ОГЭ и ЕГЭ, а вторая (краткая) послужит для решения задач.

Скачать шпаргалку со всеми формулами и определениями по физике за 7 класс (мелко на одной странице).

Для тех, кто находится на домашнем обучении или вынужден самостоятельно изучать материал ввиду пропусков по болезни, рекомендуем также учебник по физике А. В. Перышкина с формулами за 7 класс и легкими, доступными пояснениями по всем темам. Он был написан несколько десятилетий назад, но до сих пор очень популярен и востребован.

Пятерка по физике у тебя в кармане!

Решай домашку по физике на изи. Подробные решения помогут разобраться в сложной теме и получить пятерку!

Измерение физических величин

В курсе по физике за 7 класс изучают правила измерений с использованием приборов со шкалой. Если цена деления шкалы неизвестна, узнать ее можно с помощью следующей формулы:

ЦД = (max − min) / n, где ЦД — цена деления, max — максимальное значение шкалы, min — минимальное значение шкалы, n — количество делений между ними.

Вместо максимального и минимального можно взять любые другие значения шкалы, числовое выражение которых нам известно.

Выделяют прямое и косвенное измерение:

• при прямом измерении результат можно увидеть непосредственно на шкале инструмента;

• при косвенном измерении значение величины вычисляется через другую величину (например, среднюю скорость определяют на основе нескольких замеров скорости).

Для удобства и стандартизации измерений в 1963 году была принята Международная система единиц СИ. Она регламентирует, какие единицы измерения считать основными и использовать для формул. Обозначения этих единиц также учат в программе по физике за 7 класс.

Механическое движение: формулы за 7 класс

Для того, чтобы описать движение, требуется тело отсчета, система координат, а также инструмент для измерения времени. Это составляющие системы отсчета.

Изучение механического движения в курсе по физике за 7 класс включает следующие термины:

• Перемещение тела — минимальное расстояние, которое соединяет две выбранные точки траектории движения.

• Траектория движения — мысленная линия, вдоль которой перемещается тело.

• Путь — длина траектории тела от начальной до конечной точки.

• Скорость — быстрота перемещения тела или отношение пройденного им пути ко времени прохождения.

• Ускорение — быстрота изменения скорости, с которой движется тело.

Формула скорости равномерного прямолинейного движения:

V = S / t, где S — путь тела, t — время, за которое этот путь пройден.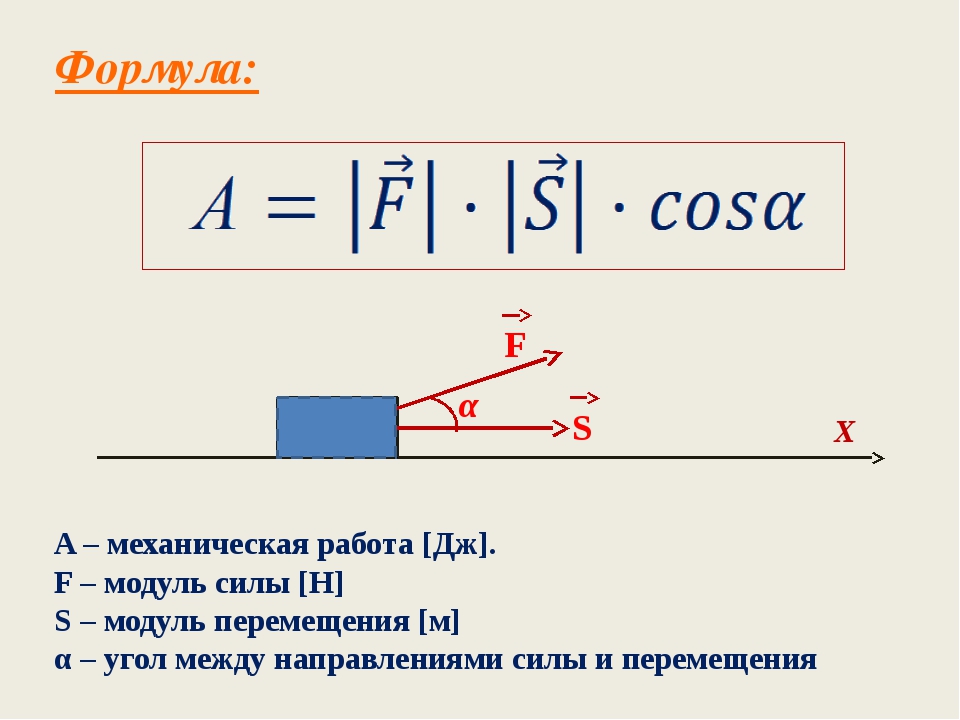

Формула скорости равномерного криволинейного движения:

где S₁ и S₂ — отрезки пути, а t₁ и t₂ — время, за которое был пройден каждый из них.

Единица измерения скорости в СИ: метр в секунду (м/с).

Формула скорости равноускоренного движения:

V = V₀ + at, где V₀— начальная скорость, а — ускорение.

Единица измерения ускорения в СИ: м/с².

Сила тяжести, вес, масса, плотность

Формулы, понятия и определения, описывающие эти физические характеристики, изучают в 7 классе в рамках такого раздела физики, как динамика.

Обратите внимание: вес тела измеряется в ньютонах, масса тела — в граммах и килограммах.

Формула веса:

P = mg, где m — масса тела, g — ускорение свободного падения.

Ускорение свободного падения возникает под действием силы тяжести, которой подвержены все находящиеся на нашей планете тела.

g = 9,806 65 м/с² или 9,8 Н/кг

Если тело находится в покое или в прямолинейном равномерном движении, его вес равен силе тяжести.

F_тяж = mg

Но эти понятия нельзя отождествлять: сила тяжести действует на тело ввиду наличия гравитации, в то время как вес — это сила, с которой само тело действует на поверхность.

Формула плотности:

ρ = m / V, где m — масса тела или вещества, V — занимаемый объем.

Единица измерения плотности в СИ: кг/м³.

Онлайн-курсы физики в Skysmart не менее увлекательны, чем наши статьи!

Механический рычаг, момент силы

О механическом рычаге говорил еще Архимед, когда обещал перевернуть Землю, если только найдется подходящая точка опоры. Это простой механизм, который помогает поднимать грузы, закрепленные на одном его конце, прилагая силу к другому концу. При этом вес груза намного превосходит прилагаемое усилие. В 7 классе физические формулы, описывающие этот процесс, изучаются в том же разделе динамики.

Рычаг находится в равновесии, если произведение силы на плечо с одной его стороны равно произведению силы на плечо с другой стороны.

Уравнение равновесия рычага:

F₁ × l₁ = F₂ × l₂

Из этого следует, что рычаг уравновешен, когда модули приложенных к его концам сил обратно пропорциональны плечам этих сил.

Формула момента силы:

M = F × l, где F — модуль силы, l — длина плеча.

Единица измерения момента силы в СИ: ньютон-метр (Н·м).

Эта формула верна, если сила приложена перпендикулярно оси рычага. Если же она прилагается под углом, такой случай выходит за рамки курса физики за 7 класс и подробно изучается в 9 классе.

Можно сказать иначе: рычаг в равновесии, если сумма моментов всех приложенных к нему сил относительно любой оси равна нулю.

М₁ + М₂ + М_n + … = 0

Давление, сила давления

Прилагая одну и ту же силу к предмету, можно получить разный результат в зависимости от того, на какую площадь эта сила распределена. Объясняют этот феномен в программе 7 класса физические термины «давление» и «сила давления».

Формула давления:

p = F / S, где F — модуль силы, S — площадь поверхности.

Единица измерения давления в СИ: паскаль (Па).

1 Па = 1 Н/м²

Понятно, что при одной и той же силе воздействия более высокое давление испытает та поверхность, площадь которой меньше.

Формулу для расчета силы давления вывести несложно:

F = p × S

В задачах по физике за 7 класс сила давления, как правило, равна весу тела.

Давление газов и жидкостей

Жидкости и газы, заполняющие сосуд, давят во всех направлениях: на стенки и дно сосуда. Это давление зависит от высоты столба данного вещества и от его плотности.

Формула гидростатического давления:

р = ρ × g × h, где ρ — плотность вещества, g — ускорение свободного падения, h — высота столба.

g = 9,8 м/с²

Единица измерения давления жидкости или газа в СИ: паскаль (Па).

Однородная жидкость или газ давит на стенки сосуда равномерно, поскольку это давление создают хаотично движущиеся молекулы. И внешнее давление, оказываемое на вещество, тоже равномерно распределяется по всему его объему.

Внешнее давление, оказываемое на жидкость или газ, рассчитывается по формуле:

p = F / S, где F — модуль силы, S — площадь поверхности.

Сообщающиеся сосуды

Если ρ₁ = ρ₂, то h₁ = h₂ и ρ₁gh₁ = ρ₂gh₂, где:

p — плотность жидкости,

h — высота столба жидкости,

g = 9,8 м/с².

Если жидкость в сообщающихся сосудах неоднородна, т. е. имеет разную плотность, высота столба в сосуде с более плотной жидкостью будет пропорционально меньше.

Высоты столбов жидкостей с разной плотностью обратно пропорциональны плотностям.

Если под поршнем 1 образуется давление p₁ = f₁/s₁, а под поршнем 2 будет давление p₂ = f₂/s₂, то, согласно закону Паскаля, p₁ = p₂

Следовательно,

Силы, действующие на поршни гидравлического пресса F₁ и F₂, прямо пропорциональны площадям этих поршней S₁ и S₂.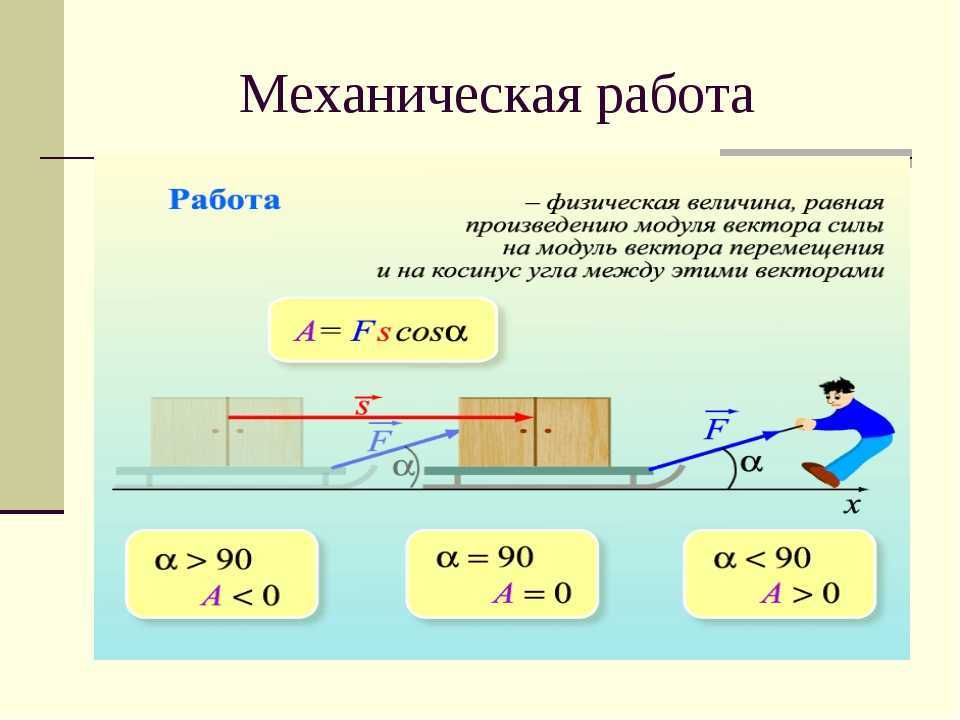

Другими словами, сила поршня 1 больше силы поршня 2 во столько раз, во сколько его площадь больше площади поршня 2. Это позволяет уравновесить в гидравлической машине с помощью малой силы многократно бóльшую силу.

Закон Архимеда

Формула архимедовой силы:

F_a = ρ × g × V, где ρ — плотность жидкости, V — объем погруженной части тела, g — ускорение 9,8 м/с².

Закон Архимеда помогает рассчитать, как поведет себя тело при погружении в среды разной плотности. Верны следующие утверждения:

• если плотность тела выше плотности среды, оно уйдет на дно;

• если плотность тела ниже, оно всплывет на поверхность.

Другими словами, тело поднимется на поверхность, если архимедова сила больше силы тяжести.

Работа, энергия, мощность

Формула работы в курсе физики за 7 класс:

A = F × S, где F — действующая сила, S — пройденный телом путь.

Единица измерения работы в СИ: джоуль (Дж).

Такое понятие, как мощность, описывает скорость выполнения механической работы. Оно говорит о том, какая работа была совершена в единицу времени.

Формула мощности:

N = A / t, где A — работа, t — время ее совершения.

Также мощность можно вычислить, зная силу, воздействующую на тело, и среднюю скорость перемещения этого тела.

N = F × v, где F — сила, v — средняя скорость тела.

Единица измерения мощности в СИ: ватт (Вт).

Тело может совершить какую-либо работу, если оно обладает энергией — кинетической и/или потенциальной.

• Кинетической называют энергию движения тела. Она говорит о том, какую работу нужно совершить, чтобы придать телу определенную скорость.

• Потенциальной называется энергия взаимодействия тела с другими телами или взаимодействия между частями одного целого. Потенциальная энергия тела, поднятого над Землей, характеризует, какую работу должна совершить сила тяжести, чтобы опустить это тело снова на нулевой уровень.

Таблица с формулами по физике за 7 класс для вычисления кинетической и потенциальной энергии:

Для того, чтобы понять, какая часть совершенной работы была полезной, вычисляют коэффициент полезного действия или КПД. С его помощью определяется эффективность различных механизмов, инструментов и т. д.

Формула для расчета КПД:

где А_п— полезная работа, А_з— затраченная работа.

КПД выражается в процентах и составляет всегда меньше 100%, поскольку часть энергии затрачивается на трение, повышение температуры воздуха и окружающих тел, преодоление силы тяжести и т. д.

Удачи на экзаменах!

Яна Кононенко

К предыдущей статье

Закон Джоуля-Ленца

К следующей статье

Диффузия

Получите индивидуальный план обучения физике на бесплатном вводном уроке

Премиум

На вводном уроке с методистом

1. Выявим пробелы в знаниях и дадим советы по обучению

2. Определим уровень и подберём курс

3. Расскажем, как 
   проходят занятия

Формула работы в физике

Содержание:

• Определение и формула работы
• Элементарная работа
• Работа силы на конечном участке траектории
• Единицы измерения работы
• Примеры решения задач

Определение и формула работы

Определение

В том случае, если под воздействием силы происходит изменение модуля скорости движения тела, то говорят о том, что сила
совершает работу. {2}}{2}(1)$$

Действие силы на материальную точку можно охарактеризовать не только с помощью изменения скорости движения тела, но при помощи
величины перемещения, которое совершает рассматриваемое тело под действием силы
($\bar{F}$).

Элементарная работа

Элментарная реабота $(\delta A)$ некоторой силы
$\bar{F}$ определяется как скалярное произведение:

$$\delta A=\bar{F} \cdot d \bar{r}=F \cdot d s \cdot \cos \alpha(2)$$

$\bar{r}$ радиус – вектор точки, к которой приложена сила,
$\bar{r}$ —
элементарное перемещение точки по траектории,
$\alpha$ – угол между векторами
$d s=|d \bar{r}|$ и $d \bar{r}$. Если
$\alpha$ является тупым углом работа меньше нуля, если угол
$\alpha$ острый, то работа положительная, при
$\alpha=\frac{\pi}{2} \delta A=0$

В декартовых координатах формула (2) имеет вид:

$$\delta A=F_{x} d x+F_{y} d y+F_{z} d z(3)$$

где F_x,F_y,F_z – проекции вектора
$\bar{F}$ на декартовы оси. {n} \bar{F}_{i} \bar{v}_{i} d t(5)$$

где проводится суммирование элементарных работ всех сил, dt – малый промежуток времени, за который совершается элементарная работа
$\delta$ над системой.

Результирующая работа внутренних сил, даже если твердое тело движется, равна нулю.

Пусть твердое тело вращается около неподвижной точки — начала координат (или неподвижной оси, которая проходит через эту точку).
В таком случае, элементарная работа всех внешних сил (допустим, что их число равно n), которые действуют на тело, равна:

$$\delta A=\bar{M} \bar{\omega} d t=\bar{M} d \bar{\varphi}(6)$$

где $\bar{M}$ – результирующий момент сил относительно точки вращения,
$d \bar{\varphi}$ – вектор элементарного поворота,
$\bar{w}$ – мгновенная угловая скорость.

Работа силы на конечном участке траектории

Если сила выполняет работу по перемещению тела на конечном участке траектории его движения, то работа может быть найдена как:

$$A=\int_{0}^{s} \bar{F} \cdot d \bar{r}(7)$$

В том случае, если вектор силы – величина постоянная на всем отрезке перемещения, то:

$$A=F_{\tau} \cdot s$$

где $F_{\tau}=F \cos \alpha$ – проекция силы на касательную к траектории. {4}$$

Ответ. n=4

Читать дальше: Формула силы Ампера.

Что такое формула работы? Примеры

Формула работы используется для расчета работы. Прежде чем мы выучим формулу, давайте вспомним, что означает работа. Говорят, что работа совершается, когда мы прикладываем силу к объекту, и объект испытывает перемещение. Если перемещение в направлении действия силы равно нулю, то совершенная работа равна нулю. Формула работы используется для расчета работы, совершаемой при перемещении объекта. Давайте узнаем больше о формуле для работы вместе с решенными примерами в следующем разделе.

Что такое формула работы?

Формула работы используется для расчета работы, затраченной на перемещение любого объекта. Работа есть произведение приложенной силы и перемещения в направлении действия силы. Работа есть скалярное произведение двух векторов: силы и перемещения. Таким образом, работа является скалярной величиной.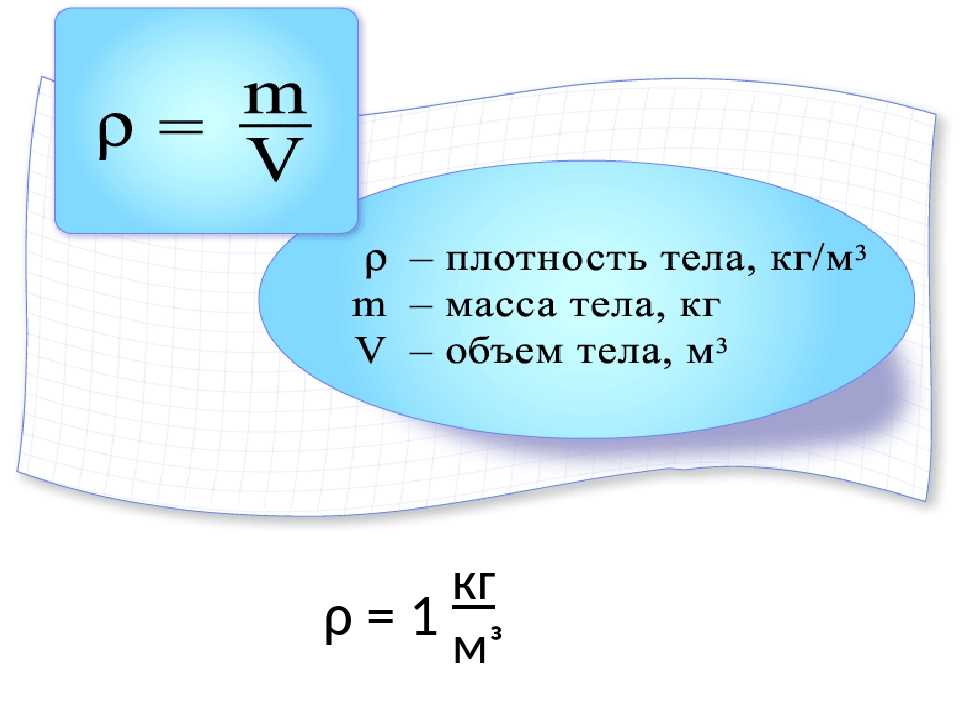 Единицей работы в системе СИ является Джоуль (Дж).

Формула работы

Формула работы может быть выражена следующим образом:

W = F.d

Вт = (Fcos θ)d

Где,

• Вт = выполненная работа
• F = Величина приложенной силы
• d = Величина смещения в направлении действия силы.
• θ = угол между векторами: силы и перемещения

Единицей работы в системе СИ является Джоуль (Дж). Если совершена работа в 1 джоуль, то формула для работы будет следующей: 1 Дж = 1 Н·м

Вывод формулы работы

Рассмотрим блок, помещенный на горизонтальном полу без трения, на который действует постоянная сила F, благодаря которой этот блок перемещается на расстояние d по прямой линии в направлении действия силы.

В общем случае работа силы F равна изменению кинетической энергии ² -u ² )

Применение v ² -u ² = 2as

W = (1/2)m(2as)

W = maston’s

3 закон), таким образом, W = Fs. (s=d=перемещение)

Теперь, если эффективная составляющая силы вдоль направления перемещения Fcosθ отвечает за перемещение любого объекта в заданном направлении, то работа, совершаемая силой F при перемещении тела на перемещение d есть, W=(|F|cosθ)|d|

Хотите найти сложные математические решения за считанные секунды?

Воспользуйтесь нашим бесплатным онлайн-калькулятором, чтобы решить сложные вопросы. С Cuemath находите решения простыми и легкими шагами.

Записаться на бесплатный пробный урок

Примеры использования формул для работы

Пример 1: 10 ньютонов сила приложена к телу, что смещает его на 2 метра. Вычислите работу, выполненную по формуле работы.
Решение: 

Чтобы найти: Работа выполнена

Дано: Сила (F) = 10 Н

Перемещение (d) = 2 м

Используя формулу для работы,

W = F.d

= (10)(2)

= 20 Нм

: 9005 Ответ Работа Нм совершается, когда сила в 10 ньютонов перемещает тело на 2 метра.

Пример 2:  Кули на вокзале несет сумку массой 100 Н на некоторое расстояние. Вычислите работу, которую совершает кули над сумкой, используя формулу работы.
Решение:

Найти работу, выполненную кули.

Дано: Вес мешка = 100 Н

Кроме того, вес мешка будет действовать в вертикальном направлении, а его движение будет происходить в горизонтальном направлении. Значит, смещение мешка в направлении действия силы (веса) равно нулю.

d = 0

Используя формулу для работы,

W = F.d

= (100)(0)

= 0 Дж

Ответ: Работа, выполненная кули на мешке, равна нулю.

Пример 3: Рассчитайте работу, выполненную силой при перемещении объекта на расстояние 7 м, если объект протаскивается горизонтально по поверхности под действием силы 150 Н, действующей параллельно поверхности.
Решение:

Найти: Работа силы при перемещении тела на расстояние 7 м

Дано: F = 150 Н, d = 7 м

Поскольку F и d направлены в одном направлении,

θ = 0, [θ — угол действия силы к направлению движения]

W = F × Cos θ × d

= 150× 7 × Cos 0

= 1050 Дж [Поскольку Cos 0 = 1]

Ответ: Работа, совершаемая силой при перемещении объекта, равна 800 J.

Часто задаваемые вопросы о формуле работы

Что такое формула работы?

Формула работы определяется как формула для расчета работы, выполненной при перемещении объекта. Совершенная работа равна произведению величины приложенной силы на расстояние, которое тело перемещает из своего начального положения в конечное. Математически проделанная работа Формула задается как W = Fd 

Какие существуют версии формулы работы?

Математически концепция выполненной работы W равна силе f, умноженной на расстояние (d), то есть W = f. d и если сила приложена под углом θ к смещению, то выполненная работа рассчитывается как W = f . д потому что θ.

Каковы применения формулы работы?

Формула работы имеет множество применений, например, для вычисления выполненной работы, силы или перемещения в любой задаче.

Что такое d в рабочей формуле?

В рабочей формуле W = F. d, d — это смещение, на сколько объект сместился со своего начального места.

Формула работы: физическое уравнение с примерами

В физике говорят, что сила совершает работу , если приложение силы смещает объект в направлении действия силы. Другими словами, работа эквивалентна приложению силы на расстоянии. Объем работы, которую совершает сила, прямо пропорционален тому, насколько далеко эта сила перемещает объект. Общая формула для работы и для определения количества работы, выполненной над объектом:

• Вт = F × D × cos(Θ)

где Вт — количество работы, F — вектор силы, а D — модуль перемещения угол между вектором силы и вектором смещения. Единицей работы в системе СИ является джоулей ( Дж ), а его размеры равны кг•м ² /с ² . Другой способ понять это состоит в том, что один джоуль эквивалентен количеству энергии, передаваемой, когда сила в один ньютон перемещает объект на расстояние в один метр.

Формула работы

Всякий раз, когда сила перемещает объект, мы говорим, что работа была выполнена. Когда мяч катится с холма под действием силы тяжести, когда вы поднимаете свой рюкзак с земли, когда внутренний двигатель вашего автомобиля прикладывает силу, заставляющую ваши колеса двигаться; все эти события связаны с силой, перемещающей объект на расстояние, и поэтому требуют некоторой работы. В тех случаях, когда к объекту приложена сила, но он не перемещается, работа не совершается. Таким образом, сила человека, толкающего стену небоскреба, не совершает никакой работы, поскольку небоскреб не движется. Рассмотрим несколько простых примеров, иллюстрирующих понятие работы.

Примеры задач

(1)

К ящику массой 15 кг в горизонтальном направлении приложена сила в 100 ньютонов, которая перемещает его на 5 метров по горизонтали. Сколько работы было сделано?

В этом случае мы знаем, что сила равна 100 Н, а расстояние – 5 метров. Мы также знаем, что, поскольку сила приложена в том же направлении, что и смещение, Θ равно 0. Таким образом, мы подставляем эти значения в наше уравнение

и получим:

• Вт = 100(5)cos(0)= 500 Дж

Итак, сила в 100 Н совершила 500 джоулей работы

(2)

На столе лежит двухкилограммовая книга. К книге приложена сила 64 Н под углом 120° к горизонтали, которая перемещает книгу на 3 м в горизонтальном направлении. Сколько работы было сделано?

В данном случае мы знаем силу 64 Н и расстояние 3 м. Мы также знаем, что между углом направления приложенной силы и направлением движения существует угол 120°. Таким образом, подставив эти значения в наше удобное уравнение, мы получим:

• W = 64(3)cos(120)= 156,32 Дж

Таким образом, сила 64 Н под углом 120° выполнила 7 156,32 м 8 м 8 901 работы по перемещению книги 9001

(3)

Линда поднимает чемодан с усилием 300 Н на 3 лестничных пролета на общую высоту 16 метров. Затем она толкает чемодан с силой 100 Н оставшиеся 8 метров до своего гостиничного номера. Сколько работы было сделано за всю ее поездку?

Этот вопрос требует 2 отдельных шагов. Ее поездка состоит из двух основных частей, поэтому мы можем рассчитать работу, проделанную для каждой части в отдельности, а затем объединить два значения, чтобы получить общий объем выполненной работы. В первой части своего пути она прикладывает силу 300 Н, чтобы переместить чемодан на 16 метров по вертикали, поэтому количество выполненной работы равно:

• Вт ₁ = 300(16)cos(0)= 4800 Дж

Таким образом, в первой части пути было потрачено 4800 Дж. Что касается второй части, мы знаем, что сила в 100 Н переместила чемодан по горизонтали на 8 метров, поэтому общая работа, выполненная на втором участке пути, равна:

• Вт ₂ =100(8)cos(0) = 800 Дж

Объединение двух значений из каждой части поездки дает:

• Вт _Всего = W ₁ + W ₂ = 4800 + 800 = 5600 Joules

So Trable Courss of Linda

.

Отношение работы/энергии

Три основных уравнения, представляющие отношения между энергией, работой и силой.

Работа и энергия в физике тесно связаны. В соответствии с принципом работы-энергии увеличение кинетической энергии твердого тела вызывается равной работой, совершаемой над этим телом силой, приложенной к этому телу. В более математических терминах отношение можно выразить следующим образом:

• W =  KE _{конечное} −KE _{начальное}

, где KE означает кинетическую энергию. Другими словами, изменение кинетической энергии тела равно работе, совершенной над этим телом. В общем, формула для кинетической энергии объекта:

• KE = (1/2) кг*в ²

, где v обозначает скорость объекта. Единицей кинетической энергии является та же единица работы, что и джоуль. Давайте рассмотрим некоторые задачи, чтобы изучить эти математические отношения.

 (4)

Осел и Дидди Конг сидят в 90-килограммовой вагонетке, которая изначально движется горизонтально со скоростью 5 м/с. Носорог Рэмби толкает вагонетку сзади и ускоряет ее, так что теперь она движется со скоростью 11 м/с. Сколько работы Рэмби проделал с вагонеткой?

Чтобы решить эту задачу, нам сначала нужно вычислить начальную кинетическую энергию вагонетки и ее конечную кинетическую энергию. Зная эти значения, мы можем определить общий объем работы. Мы знаем как скорость, так и массу вагонетки, поэтому мы можем определить общую кинетическую энергию в начале и в конце. Начальная кинетическая энергия вагонетки:

• КЭ _{начальная} =(1/2)(90)(5) ² =  1125 Дж

Конечная кинетическая энергия вагонетки равна )(90)(11) ² = 5445 Дж

Таким образом, общая работа, выполненная на вагонетке, равна 5545−1125= 4420 Дж .

«Наука — это знание последствий и зависимости одного факта от другого». – Томас Гоббс

(5)

Автомобиль массой 1300 кг движется со скоростью 18 м/с. Если над автомобилем совершить работу 60000 джоулей, какова будет его конечная скорость?

Вопрос потребует немного алгебры.